Massimo Finocchiaro Castro, Mediterranean University of Reggio Calabria, Italy
Calogero Guccio, University of York, United Kingdom
Domenica Romeo, Mediterranean University of Reggio Calabria, Italy
Earth’s Orbits at Risk
The Economics of Space Sustainability
9. An efficiency analysis of space launch activities
Abstract
Investments in space programmes appear to bring significant economic benefits to society, but they pose new challenges. This chapter proposes the first methodological approach empirically investigating the efficiency of satellite launches. Specifically, it proposes a model for evaluating satellite launch activity and apply it to a sample of satellites.
Introduction
In the last few years, countries and commercial firms have become increasingly interested in space activities for civil, military and commercial purposes. As has been shown in the economic impact assessment study released by the US National Aeronautics and Space Administration (NASA) (NASA, 2019[2]), investments in space programmes can bring substantial economic benefits to society. More directly, space activities positively affect gross domestic product, by creating employment and generating revenues (OECD, 2019[3]). To put things in perspective, during fiscal year 2019, NASA’s activities produced more than USD 64.3 billion in total economic output, supporting thousands of jobs nationwide (NASA, 2019[2]).1
Space-based infrastructures are essential for citizens’ everyday lives. Data resulting from space observation are used for weather forecasting, climate monitoring (Cheng et al., 2006[4]) and, above all, telecommunications. For all these reasons, starting from the launch of Sputnik 1, the use of Earth’s orbits has expanded globally (Liou and Johnson, 2006[5]), mainly boosted by lower launch costs and foreseen returns. Since 2010, NASA has recorded on average roughly 80 launches per year (Liou, 2017[6]). Specifically, lower orbits are overpopulated due to a considerable rise in constellation satellites, replacing single satellites (Chrystal, Mcknight and Meredith, 2018[7]). The accumulation of man-made objects, defined as orbital debris, dramatically challenges the long-term sustainability of space operations, posing considerable risks to human space flight and robotic missions (Liou and Johnson, 2006[5]). Beyond the existing costs of satellites protection and mitigation (see, for example, Rossi et al. (2017[8]), the costs resulting from accidental collisions with debris deserve special attention. First, collisions generate additional debris, leading to the so-called Kessler Syndrome of self-generating collisions (Rossi, Valsecchi and Farinella, 1999[9]; Adilov, Alexander and Cunningham, 2020[10]). In fact, projections to simulate the future debris patterns show that after 2055, even assuming no further satellites launches, the satellite population will increase due to the generation of new collision fragments, exceeding the quantity of decaying debris (Liou and Johnson, 2006[5]). Second, satellites’ random collisions with debris not only would require spacecraft replacement and trigger launch delays but, most importantly, it could result in data loss, with disastrous economic consequences for satellite communications (OECD, n.d.[1]).
Given the importance of space activities in a variety of areas, assessing the balance between revenues and the costs related to launches of satellites might be of some interest. Specifically, estimating satellite efficiency could fill a notable gap in the research literature. At the base of each economic activity stands the relationship between revenue and cost, or, to put it differently, between input and output leading to efficiency analysis. The pursuit of high efficiency levels is the main goal of any organisation. In that regard, we believe that filling this knowledge gap in the space economy framework deserves attention.
We therefore propose a model to evaluate satellite launch activity and apply it to a sample of satellites. To assess the relative efficiency of satellite launch activity, we employ an estimation technique – data envelopment analysis (DEA) – which, due to its methodological properties, is one of the most common approaches for assessing the efficiency of organisations. In general terms, DEA is a mathematical programming technique designed to evaluate the relative efficiency for a group of comparable observations (decision‑making units, DMUs), which is capable of handling multiple inputs and outputs without requiring a priori assumptions of a specific functional form on production technologies and the relative weighting scheme.
Following the DEA approach, we will consider launched satellites as DMUs to estimate the efficiency of their life cycle, satellite mass (i.e. a proxy for the satellite’s dimensions and then for the number of debris objects it might generate following a collision) and mission costs as inputs, and expected life as an output. Though coping with a very limited amount of available data (i.e. 37 satellites on the whole), our results can inform interesting policy strategies. Our findings show that overall average efficiency is quite low and that it could significantly be improved by studying launches according to user, purpose and class of orbit, showing how they largely affect mission efficiency and, even more relevant, future debris creation. Consequently, regulations on satellite composition (for instance reducing the launch mass) or on design could increase efficiency levels. Additionally, identifying market solutions to make reliable data available and accessible could help further improve the analysis.
Methods and data
Methodological framework
As previously mentioned, to perform our empirical exercise, we will employ the DEA approach, which is a non-parametric mathematical programming technique that can be oriented to minimise input values or maximise output (Coelli, 1998[11]).DEA measures productive efficiency through the estimation of a frontier envelopment surface for all DMUs by using linear programming techniques. In doing so, it allows identifying best practices and comparing each DMU with the best possible performance among peers, rather than just with the average. Once the reference frontiers have been defined, it is possible to assess the potential efficiency improvements available to inefficient DMUs if they were producing according to the best practice of their benchmark peers. From an equivalent perspective, these estimates identify the necessary changes that each DMU needs to undertake to reach the efficiency level of the most successful DMU (Fried, Knox Lovell and Schmidt Shelton, 2008[12]). In addition, whereas DEA is, at the beginning, run under the constant returns to scale, it can be reformulated to account for variable returns to scale as well (Banker et al., 1988[13]).
The input-oriented approach fits our case study nicely, measuring the radial reduction in input for a given output as the distance (efficiency score) between the observed and most efficient DMU. Our data set calls for such an approach, where for a given output level, the efficiency can be reached minimising the inputs.
Illustrating this point,2 consider n DMUs for evaluation; a DEA input-oriented efficiency score hi is calculated for each DMU, which solves the following programme for i = 1,..., n using the constant returns to scale (CRS) assumption.3
xi and yi are the input and output, respectively, for the ith DMU; X is the matrix for the input, Y is the matrix for the output, and λ is a nx1 vector of variables. The model (1) can be modified to account for variable returns to scale (VRS) by adding the convexity constraint eλ = 1 where e is a row vector with all elements unity, which distinguishes between technical efficiency (TE) and scale efficiency (SE).
DEA is a well-established and useful technique for measuring efficiency in several sector activities (for a comprehensive review, see (Liu et al., 2013[14]). The reasons for the widespread use of DEA are summarised as follows: it can handle multiple inputs and outputs without a priori assumptions for a specific functional form of production technologies, it does not require a priori a relative weighting scheme for the input and output variables, it returns a simple summary efficiency measurement for each DMU, and it identifies the sources and levels of relative inefficiency for each DMU.
However, DEA is an estimation procedure that relies on extreme points: it may be extremely sensitive to data selection, aggregation and model specification. Typically, the selection of input and output variables is a major issue for efficiency measurements. The principal strengths of DEA, which include no a priori knowledge requirement for functional relationships, can be fully exploited under the premise that the input and output variables are relevant and sufficiently fair for all the DMUs considered.
Another problem common to DEA studies is the relatively small number, n, of DMU with respect to the space dimension d (i.e. the number of input and output variables in the efficiency analysis) and the reliability of the results from the DEA model. However, for a given sample size, the rate of convergence depends on the space dimension d.4 This issue clearly represents a potential limitation of our work that may be solved only when more data are available. Notwithstanding, we do believe that our analysis represents a first sound step to the analysis of launch efficiency.
Finally, since DEA does not allow for any statistical inference and measurement error, Simar and Wilson (2000[15]; 1998[16]) introduced a bootstrapping methodology to determine the statistical properties of DEA estimators.5 Thus, the bootstrapping algorithm (Simar and Wilson, 2000[15]) is used in this chapter to control for consistency among the efficiency estimates.6
Data
Our sample has been built on the publicly accessible Union of Concerned Scientists (UCS) Satellite Database, which contained 4 550 entries on 1 September 2021 (UCS, 2022[17]). First, we selected the launches with complete information on a satellite’s expected lifetime (measured in years), Expectedlifetimeyrs, which represents our output. Once satellites with such missing data were removed, we searched for those variables chosen as input: the launch mass, Launchmasskg, and the mission cost, Cost. Whereas the launch mass was directly taken form the UCS Satellite Database, the cost was taken from different sources provided in the UCS data set (e.g. spaceflightnow.com).
Hence, we restricted our data set to 37 satellites, representing the DMUs under investigation. Table 9.1 provides a first description of a sample composition. At a first glance, it appears that launches span quite a wide period, ranging from 2006 to 2020, although most of the launches took place in the last five years and that several countries or multinational agencies have been involved in the launches forming the sample under study. In detail, eight countries (Argentina, Australia, Canada, France, Germany, India, Korea and the United States) and two international agencies (the European Space Agency [ESA] and the European Organisation for the Exploitation of Meteorological Satellites [EUMETSAT]) are listed as satellite registration countries/organisations.
Table 9.1. Sample composition
Notes: DMU: decision-making unit; NR: the satellite has never been registered with the United Nations; ESA: European Space Agency; EUMETSAT: European Organisation for the Exploitation of Meteorological Satellites.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Moreover, the UCS data set includes additional basic information about the satellites and their orbits. Specifically, for each of the satellites, it provides the country of owner, the users and its purpose. Additional relevant satellite characteristics are reported in Table 9.2.
Table 9.2. Users, purpose and class of orbit
Note: DMU: decision-making unit; LEO: low-earth orbit; MEO: medium-earth orbit; GEO: geostationary earth orbit.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Data show that most of the satellites (62%) are in the low-earth orbit (LEO), 5% are in the medium-earth orbit, 30% in the geostationary Earth orbit (GEO) and the remaining 3% in the high elliptical orbit. Satellite use can be divided into governmental (59%), civil (3%), military (8%), commercial (16%) or mixed (13%). Regardless of the orbit (with the only exception of medium-earth orbit, where there are only commercial satellites) their largest employment is for governmental purposes. Finally, as far as their purpose is concerned, the largest share of the satellites localised in the LEO (78%) are developed for earth observation, whereas most of the satellites localised in the GEO (82%) are developed for communication.
Table 9.3 reports the values of the three variables included in our DEA model for each DMU. The DMUs are ordered according to their expected life from the smallest to the largest.
Table 9.3. Inputs and outputs
Note: DMU: decision-making unit.
Source: Calculations based on data provided by the Union of Concerned Scientists.
As we can observe, data are very heterogeneous across the DMUs. This issue can be also noted by looking at Table 9.4, referring to the average values of the sample. Launch mass (expressed in kilogrammes [kg]) ranges from 4 kg to 6 405 kg, mission costs (USD millions) go from USD 60 million to USD 11 700 million, while the expected lifetime varies from 4 months to 20 years. Data heterogeneity is also shown by the high standard deviations for both inputs and output.
Table 9.4. Sample statistics
Source: Calculations based on data provided by the Union of Concerned Scientists.
Results
Unfortunately, the available data are quite incomplete, and we acknowledge that this represents a potential limitation to our analysis. As mentioned above, the available data moved us to choose satellite mass and mission cost as inputs and satellite expected life as output. Thus, it is reasonable to opt for an input‑oriented estimation model, which is more consistent with the objective of the analysis. The rationale for such a choice is: for a given expected lifetime, the less resources in terms of mass launched into space and mission economic resources employed, the more efficient the satellite is.
This feature is relevant under a different perspective. A smaller mass implies less debris caused in the event of a collision. Hence, minimising satellites’ mass may positively affect efforts to reduce the number of debris objects, and increase the satellites’ expected lifetime. In all our estimates, each satellite represents our DMU. Furthermore, we will employ the well-known DEA estimator, put forward by Charnes, Cooper and Rhodes (1978[18]), measuring the efficiency in terms of Farrell (1957[19]) input distance functions, which are the reciprocals of the Shephard (1970[20]) input efficiency measures. Then, for a point contained within the convex hull of the reference observations, the returned efficiency scores will be between 0 and 1. The larger the efficiency score, the higher the efficiency of the DMU. Furthermore, we assume constant returns to scale. To account for possible bias in the estimates and the presence of outliers, we will also perform the bootstrap confidence interval for efficiency estimates (Simar and Wilson, 2000[15]). Table 9.5 reports the efficiency estimates for each DMU. Column 2 shows the original efficiency scores; Columns 3 and 4 provide the bias and bias-corrected efficiency scores. Columns 5 and 6 report the 95% confidence intervals for the bias-corrected efficiency scores. As can be seen, the value reported in the second column falls beyond the upper bound of the confidence intervals, revealing the presence of bias in the estimates. Both the levels of bias and bias-corrected estimates vary significantly across the DMUs. The greatest difference between the original and the bias-corrected efficiency scores is 0.40525 (DMU 4).
Table 9.5. Efficiency estimates
Note: DMU: decision-making unit; DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Table 9.6 displays the average values. The bias-corrected efficiency scores range from 0.71750 to 0.01596, showing a remarkably high degree of heterogeneity among the DMUs. Also, the mean efficiency score across the sample is 0.2611, showing that, on average, inputs could be reduced altogether by roughly 74% to get full efficiency. Overall, the efficiency decreased slightly with a mean drop of slightly more than 8%.
Table 9.6. Summary statistics of the efficiency estimates
Note: DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
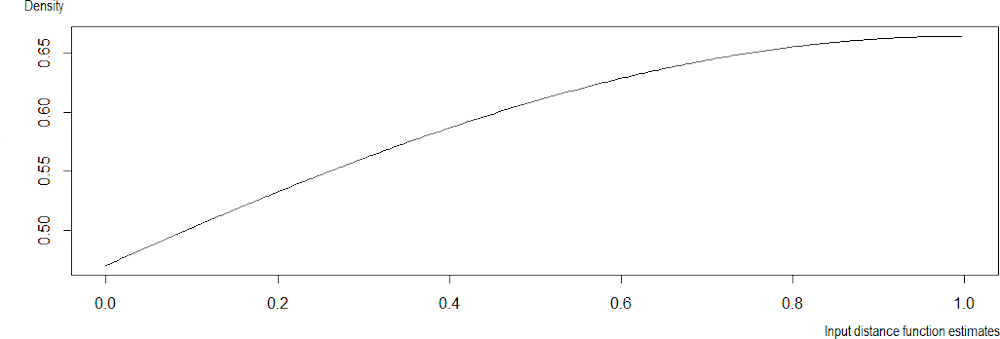
Figure 9.1 reports the Kernel density estimates of the efficiency scores that rely on the reflection method (Simar and Wilson, 2008[21]). The results are not significantly different from those reported in Table 9.6.
The presence of bias in the original efficiency scores reported in Table 9.6 could be further investigated by decomposing the sample according to the homogeneous characteristics of satellites. To do so, the following tables cluster the efficiency estimates according to user, purpose and class of orbit. Table 9.7 reports the DMUs clustered by user. In more than half of the observations, governments are the user, with an average bias-corrected efficiency score of 0.2628, with a small bias of 0.0798.
Figure 9.1. Kernel density of the data envelopment analysis efficiency estimates
Table 9.7. Efficiency estimates by user
Note: DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Inversely, Table 9.8 refers to the clustering by satellites’ purpose. In this case, there are two main groups. The first and more numerous is related to Earth observation (54% of the sample), showing an average bias-corrected efficiency score of 0.1799, with a very small bias of 0.0419. The second group refers to communications, showing an average bias-corrected efficiency score of 0.4117, with a quite significant bias of 0.1368.
Table 9.8. Efficiency estimates by purpose
Note: DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Finally, Table 9.9 regards the cluster according to the class of orbit of the satellites. In this cluster, there are also two main groups. The first refers to LEO, showing an average bias-corrected efficiency score of 0.1928, with a quite small bias of 0.0577, whereas the second cluster refers to GEO, reporting an average bias-corrected efficiency score of 0.3720, with a remarkable bias of 0.1217.
Table 9.9. Efficiency estimates by class of orbit
Notes: DEA: data envelopment analysis; x = Not applicable.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Looking in depth at the results reported in the previous tables, it seems reasonable to perform new estimates focusing only on the most homogeneous groups of DMUs to mitigate the bias. Thus, the following tables report the efficiency estimates for the subsamples referring to earth observation and communications.
Table 9.10 reports the efficiency estimates for the subsample of communications satellites. The results show a quite remarkable increase in the average bias-corrected efficiency scores of the subsample, as compared to the results for communications satellites in Table 9.8 moving from 0.4117 to 0.5275. Also, the bias has significantly decreased, from 0.1368 to 0.0970. It thus appears that we have been able to somehow mitigate the negative effect of the DMUs’ heterogeneity on efficiency levels.
Table 9.10. Efficiency estimates for the subsample of communications satellites
Note: DMU: decision-making unit; DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Inversely, Table 9.11 shows the efficiency estimates for the subsample of earth observation satellites. In this case, the average bias-corrected efficiency score has tripled, from 0.1799, as reported in Table 9.8, to 0.5401, while keeping the bias at a very low level (0.0835). As said before, running estimates on a subsample to keep heterogeneity at a minimum has dramatically helped boost bias-corrected efficiency levels.
Table 9.11. Efficiency estimates for the subsample of earth observation satellites
Note: DMU: decision-making unit; DEA: data envelopment analysis.
Source: Calculations based on data provided by the Union of Concerned Scientists.
Conclusions
Space activities are becoming crucial for many areas such as meteorology, navigation, communication and earth observation. For this reason, most countries are increasingly investing in the space sector to improve their space-launching capabilities.
Considering the growing importance of the space sector in everyday life, especially in the long and medium terms, assessing the efficiency of space activities could be of interest to policy makers. Thus, we aimed to fill the gap in the space literature by providing an efficiency analysis using the DEA technique. Specifically, by using a subsample of the UCS Satellite Database, we considered 37 satellites, launched between 2006 and 2020, as our decision-making units, their launch mass and mission cost as inputs and their expected life expressed in years as output, for our input-oriented approach. Also, the mean efficiency score across the sample is 0.2611, showing that on average, inputs could be reduced altogether by roughly 74% to reach full efficiency. In a second step, satellites were clustered according to their users, purposes and class of orbit respectively, to account for data heterogeneity. Then, the efficiency analysis was conducted for two subsamples based on their purposes: Earth observation and communications. For earth observation, the results show a quite remarkable increase in the average bias-corrected efficiency scores of the subsample, moving from 0.4117 to 0.5275. Also, the bias significantly decreased, from 0.1368 to 0.0970. Focusing on communications, the average bias-corrected efficiency score tripled, from 0.1799 to 0.5401, while keeping the bias at a very low level (0.0835). Hence, it appears that the communications satellites are those where inputs are more efficiently employed, keeping the expected lifetime constant.
From a policy perspective, it could be worth designing interventions that improve satellite efficiency by working on the launch mass which, in its turn, can affect the mission cost. To incentivise the space sector to focus on mission design, policy makers could introduce soft regulatory tools such as guidelines on satellite composition, driving agents to conform to standards on the dimensions or on the materials used to build the satellites, for example. Debris mitigation and remediation policies, which have been very inconclusive so far (Hall, 2014[22]), could benefit from similar regulatory mechanisms.
However, our results should be interpreted with caution. Several limitations affect our study, the main problem being the limited available sample set due to multiple missing variables in the UCS Satellite Database. Market mechanisms that make such information available would not only make the analysis more robust, but could support the sector in detecting strategies to improve efficiency levels.
Notwithstanding, we believe that our analysis represents the first step in the efficiency analysis of satellites’ launches, placing attention on the problem of future debris creation.
References
[10] Adilov, N., P. Alexander and B. Cunningham (2020), “The economics of orbital debris generation, accumulation, mitigation, and remediation”, Journal of Space Safety Engineering, Vol. 7/3, pp. 447-450, https://doi.org/10.1016/j.jsse.2020.07.016.
[13] Banker, R. et al. (1988), “A comparison of DEA and translog estimates of production frontiers using simulated observations from a known technology”,”, in Applications of Modern Production Theory: Efficiency and Productivity, pp. 33-35, Springer, Dordrecht, https://doi.org/10.1007/978-94-009-3253-1_2.
[18] Charnes, A., W. Cooper and E. Rhodes (1978), “Measuring the efficiency of decision making units”, European Journal of Operational Research, Vol. 2/6, pp. 429-444, https://doi.org/10.1016/0377-2217(78)90138-8.
[4] Cheng, C. et al. (2006), “Satellite constellation monitors global and space weather”, EOS Transactions American Geophysical Union, Vol. 87/17, p. 166, https://doi.org/10.1029/2006EO170003.
[7] Chrystal, P., D. Mcknight and P. Meredith (2018), New Space, New Dimensions, New Challenges: How Satellite Constellations Impact Space Risk, Swiss Re Corporate Solutions Ltd, Zurich.
[11] Coelli, T. (1998), “A multi-stage methodology for the solution of orientated DEA models”, Operations Research Letters, Vol. 23/3-5, pp. 143-149, https://doi.org/10.1016/S0167-6377(98)00036-4.
[19] Farrell, M. (1957), “The measurement of productive efficiency”, Journal of the Royal Statistical Society: Series A (General), Vol. 120/3, pp. 253-281, https://doi.org/10.2307/2343100.
[12] Fried, H., C. Knox Lovell and S. Schmidt Shelton (2008), The Measurement of Productive Efficiency and Productivity Growth, Oxford University Press, New York, NY.
[22] Hall, L. (2014), “The history of space debris”, Space Traffic Management Conference, 16-18 November 2014, paper 19.
[6] Liou, J. (2017), USA Space Debris Environment, Operations, and Research Updates, 54th Session of the Scientific and Technical Subcommittee of the Committee on the Peaceful Uses of Outer Space, United Nations, 30 January-10 February, Vienna, https://www.unoosa.org/pdf/pres/stsc2012/tech-26E.pdf.
[5] Liou, J. and N. Johnson (2006), “Risks in space from orbiting debris”, Science, Vol. 311/5759, pp. 340-341, https://doi.org/10.1126/science.1121337.
[14] Liu, J. et al. (2013), “A survey of DEA applications”, Omega, Vol. 41/5, pp. 893-902, https://doi.org/10.1016/j.omega.2012.11.004.
[2] NASA (2019), Economic Impact Report FY19, National Aeronautics and Space Administration, https://www.nasa.gov/press-release/nasa-report-details-how-agency-significantly-benefits-us-economy.
[3] OECD (2019), The Space Economy in Figures: How Space Contributes to the Global Economy, OECD Publishing, Paris, https://doi.org/10.1787/c5996201-en.
[1] OECD (n.d.), OECD Science, Technology and Industry Policy Papers, OECD Publishing, Paris, https://doi.org/10.1787/23074957.
[8] Rossi, A. et al. (2017), “The H2020 project ReDSHIFT: Overview, first results and perspectives”, Proceedings of the 7th European Conference on Space Debris, https://elib.dlr.de/121525.
[9] Rossi, A., G. Valsecchi and P. Farinella (1999), “Risk of collisions for constellation satellites”, Nature, Vol. 399/6738, p. 743, https://doi.org/10.1016/j.omega.2012.11.004.
[20] Shephard, R. (1970), Theory of Cost and Production Functions, Princeton University Press, Princeton, NJ.
[21] Simar, L. and P. Wilson (2008), “Statistical inference in nonparametric frontier models: Recent developments and perspectives”, in Fried, H., C. Knox Lovell and S. Schmidt Shelton (eds.), The Measurement of Productive Efficiency and Productivity Growth, https://doi.org/10.1093/acprof:oso/9780195183528.003.0004.
[15] Simar, L. and P. Wilson (2000), “A general methodology for bootstrapping in non-parametric frontier models”, Journal of Applied Statistics, Vol. 27/6, pp. 779-802, https://doi.org/10.1080/02664760050081951.
[16] Simar, L. and P. Wilson (1998), “Sensitivity Analysis of Efficiency Scores: How to Bootstrap in Nonparametric Frontier Models”, Management Science, Vol. 44/1, pp. 49-61, https://doi.org/10.1287/mnsc.44.1.49.
[17] UCS (2022), UCS Satellite Database, https://www.ucsusa.org/nuclear-weapons/space-weapons/satellite-database (accessed on 20 March 2019).
Notes
← 1. The Moon to Mars exploration programme alone generated 69 000 jobs nationwide (NASA, 2019[2]).
← 2. For more details, see Coelli (1998[11]) and Fried, Know Lovell and Schmidt Shelton (2008[12]).
← 3. The acronyms CRS and VRS are often used with reference to the CCR and BCC models from the initials of the authors, Charnes, Cooper and Rhodes (1978[18]), Banker et al. (1988[13]).
← 4. For a numerical example of the trade-off between sample size and number of inputs and outputs used for consistency, see Simar and Wilson (2008, p. 439[21]).
← 5. The idea is to simulate a true sampling distribution by mimicking their DGP – here the outputs from DEA (Simar and Wilson, 2008[21]) – by constructing a pseudo-data set and re-estimating the DEA model with this new data set. Repeating the process many times to achieve a good approximation of the true distribution of the sampling. The Simar and Wilson (1998[16]) bootstrap procedure gives an estimated bias and the variance, which in turn provide confidence intervals. Later, Simar and Wilson (2000[15]) provided an improved and more flexible procedure that automatically corrects for biases without explicit use of a noisy bias estimator. See Simar and Wilson (2008[21]) for the technical details on the bootstrap procedures.
← 6. This procedure is also adopted because it does not assume homogeneity on the distribution of efficiency, which may be too restrictive for this analysis and may invalidate the inference on the efficiency estimates.