Bricks, Taxes and Spending

7. Housing supply responsiveness across levels of government: Novel evidence on tax and spending autonomy

Frank van Hoenselaar
oecd

Boris Cournède
oecd

Sean Dougherty
oecd

Abstract

This research explores how fiscal autonomy across governmental tiers affects housing supply amidst declining housing affordability across countries. Using unique OECD indicators, the study assesses the decentralisation of housing-related spending and property tax autonomy. While local governments often possess insights into regional needs, they often encounter "NIMBYism", where current residents resist new development. The chapter also evaluates the influence of tax autonomy, particularly regarding property taxes, on housing supply. The results indicate that countries with more local control over housing spending policies exhibit lower housing supply elasticities. In contrast, for those subnational entities that control more of their property tax base, a higher elasticity is found, potentially driven by the lure of increased tax revenues from new development. This study underscores the interplay between spending decentralisation and tax incentives, suggesting that local tax benefits might counteract opposition to housing development.

This paper was presented at the 2021 meeting of the OECD Network on Fiscal Relations across Levels of Government. It was prepared by Frank van Hoenselaar, while on secondment from the Netherlands Central Bank to the Network, together with Sean Dougherty, head of the Network Secretariat and Boris Cournède, coordinator of the OECD Horizontal Housing Project. The authors would like to thank John Muellbauer, Luiz de Mello, Federica De Pace and Jaebeum Cho for providing helpful written comments.

7.1. Introduction and main findings

Rising house prices and diminishing housing affordability are an impediment to realising an inclusive housing market. Recent OECD work shows that the affordability of housing is declining in developed countries, with households spending an increasingly larger share of their income on housing (OECD, 2021[1]). These trends tend to affect many vulnerable households. Expanding the current stock of housing is key to ensuring universal access to housing and improving housing affordability. Housing supply needs to be sufficiently elastic to ensure that the economy responds to changing housing needs in a swift manner. Earlier work by the OECD (Caldera and Johansson, 2013[2]; Cavalleri, Cournède and Özsöğüt, 2019[3]) documented a wide dispersion in the price elasticity of housing supply across OECD countries. This earlier work also provides evidence that supply elasticities in OECD countries are negatively affected by land use regulation and natural barriers, as these limit the possibilities to expand supply.

This paper contributes to the policy debate by linking the price elasticity of housing supply to a new set of indicators that capture the division of housing-related expenditure responsibilities across different layers of government. These novel indicators were recently designed by the OECD Network on Fiscal Relations and constructed based on the OECD Questionnaire on Affordable & Social Housing and Phillips (2020[4]). Over recent decades, governments have implemented policy reforms that have allocated more and more responsibilities to local governments for developing, co-ordinating and implementing housing policies. The underlying idea for these reforms is that local governments have greater knowledge of local preferences and conditions. On the flipside, however, local governments can be prone to lobbying by existing residents that dislike new construction because it can decrease the value of their homes and the attractiveness of their neighbourhoods (Fischel, 2004[5]; Hilber and Robert-Nicoud, 2013[6]; Blöchliger et al., 2017[7]). This is often termed “NIMBYism” (not in my backyard-ism).

This paper thus investigates the effect of greater decentralisation of housing responsibilities in terms of spending power on the elasticity of housing supply. The paper also investigates how the tax autonomy of local governments influences the elasticity of housing supply based on another unique set of OECD indicators developed by the Network on Fiscal Relations (Dougherty, Harding and Reschovsky, 2019[8]). Tax autonomy implies that local governments can levy their own taxes and decide on rates and tax bases themselves. In relation to housing supply, autonomy over local property taxes is especially relevant: if housing construction yields additional property tax revenues to finance local public goods, it might incentivise local governments to allow more new construction. The paper therefore investigates the relationship between the property tax autonomy of local governments and housing supply.

There is limited empirical work that aims to explain differences in housing supply elasticities across countries. More work has been done in explaining supply elasticities within countries, across regions or municipalities (Saiz, 2010[9]; Hilber and Vermeulen, 2016[10]; Green, Malpezzi and Mayo, 2005[11]). These studies show that supply elasticities tend to be lower in areas with more stringent geographic or regulatory constraints to new construction. Studying the nature of housing supply at an aggregate level has some pitfalls, as the planning system and geographic constraints typically have a local character. Studying them at an aggregate level could result in aggregation bias, because more constrained areas are averaged with less constrained areas. However, recent empirical work has shown that nationally estimated housing elasticities are tightly correlated with cross-regional averages of regionally-estimated elasticities (Bétin and Ziemann, 2019[12]). Based in part on this evidence, as well as the effect of national policies on housing supply, it is worth exploring the factors behind the cross-country variation in housing supply elasticities.

The empirical strategy of this paper builds upon earlier OECD work on housing supply elasticities (Cavalleri, Cournède and Özsöğüt, 2019[3]). It extends their model by including the spending and tax autonomy indicators. The empirical results of the paper indicate the following:

• Countries where housing policy responsibilities are more decentralised – in terms of their spending power – experience lower price elasticities of housing supply. Of the sub-components of the spending power indicator, policy autonomy exerts the largest negative impact on the supply elasticity. The results appear to be partially non-linear, with the effect becoming increasingly strong with greater decentralisation.

• Countries where subnational governments have more control over their property taxes – more property tax autonomy – and which levy a larger share of property taxes, have higher elasticities of housing supply. If local governments and communities can benefit from new construction through increased property taxes, they will be more inclined to allow new development.

The next section ‎7.2 describes the data, model and empirical strategy, then the following section ‎7.3 interprets the empirical results and discusses their implications. The final section ‎7.4 concludes.

7.2. Empirical strategy

7.2.1. Data

This paper employs the housing policy dataset developed by Cavalleri, Cournède and Özsöğüt (2019[3]). This panel dataset consists of 25 countries and quarterly data from 1980Q1 until 2017Q4. The main variables of interest are real residential investment, real house prices, construction costs, total population and real disposable income per capita. The dataset does not cover the entire period for all countries in the sample, due to limited coverage for some variables. The dataset by Cavalleri, Cournède and Özsöğüt (2019[3]) is complemented by several measures for the decentralisation of housing policies and taxation. Box ‎7.1 discusses the calculation of the spending power and tax autonomy indicators.

Box ‎7.1. Subnational spending power and tax autonomy in the housing sector

Spending power

Spending power is defined as the ability of a subnational government to control its own expenditure. The spending power indicators aim to provide more information than just the expenditure shares of subnational government by distinguishing between situations where subnational governments are merely the paying agent for the central government and where they have little independence or decision-making authority. Dougherty and Phillips (2019[13]) constructed a spending power indicator for five sectors – health, education, old age care, transportation and housing – along four dimensions:

• Policy autonomy: The extent to which subnational decision-makers exert control over main policy objectives and main aspects of service delivery.

• Budget autonomy: The extent to which subnational decision-makers exert control over the budget (e.g., is budget autonomy limited by upper-level regulation).

• Input autonomy: The extent to which subnational decision-makers exert control over the civil service (personnel management, salaries) and other input-side aspects (e.g., right to tender or contract out services).

• Output and monitoring autonomy: The extent to which subnational decision-makers exert control over standards such as quality and quantity of services delivered and devices to monitor and evaluate standards, such as benchmarking.

Among the five sectors, housing is the most decentralised. Phillips (2020[4]) uses the same concept to construct spending power indicators with a focus on affordable housing development. This indicator is based on input that OECD member countries provided via the Questionnaire on Affordable and Social Housing. The four dimensions are used to build an aggregate indicator, with 0 representing fully centralised decisions and increasing values more decentralised ones (Figure ‎7.1).

Figure ‎7.1. Composition of the spending power indicator

Source: Authors’ calculation based on data from Phillips (2020[4]).

Property tax autonomy

Starting in 1995, the OECD began to assess the tax autonomy of state or regional and local governments in OECD member countries. A taxonomy was developed to assess the degree of tax autonomy in each country. Each tax instrument used by state or local governments in a country is assigned one of twelve possible policy-based codes to indicate the extent of tax autonomy for the instrument. The results of this exercise are summarised by calculating the share of total government revenue by level of government assigned to each tax autonomy code. Property tax autonomy is calculated as the share of property taxes in a country that are gathered by subnational governments. The indicator lies between 0 and 1. Figure ‎7.2 shows the distribution of the property tax autonomy variable. From the most recent vintage, the indicators are available on an annual basis, using revenue shares to construct the indicator in the years between the three-yearly survey updates (Dougherty, Harding and Reschovsky, 2019[8]). The indicators are disseminated in the OECD Fiscal Decentralisation database.

Figure ‎7.2. Property tax autonomy (1980 – 2018)

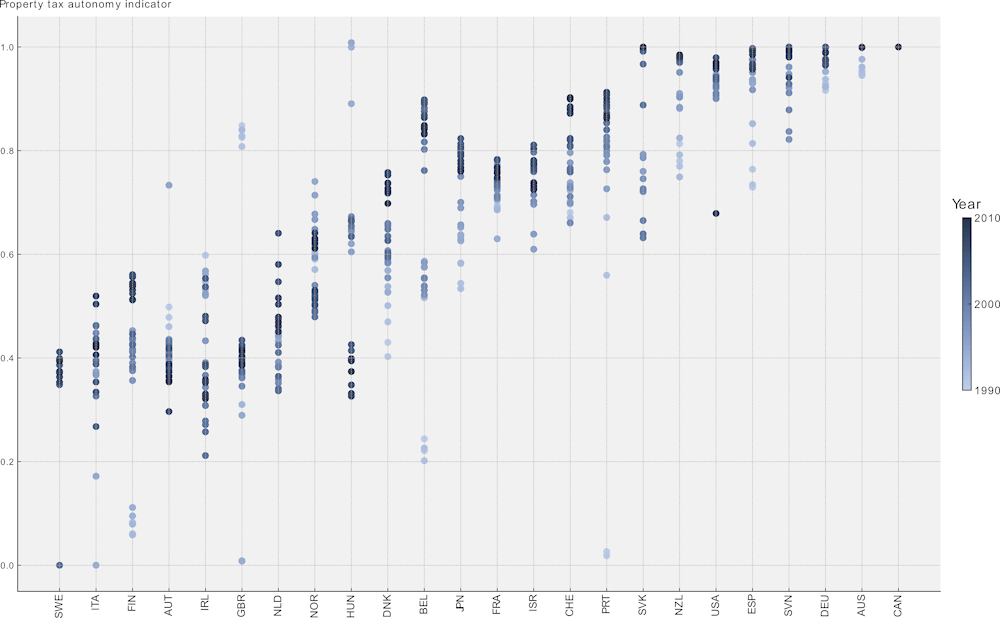
Source: ChatGPT rendering based on data from the OECD Fiscal Decentralisation Database and Revenue Statistics.

For the decentralisation of housing policies, this paper relies on the work by Phillips (2020[4]) regarding the spending power of subnational governments in the area of affordable housing. As this spending power indicator is only available for one year for each country, we need to implicitly assume that the assignment of spending power across governments has been relatively stable over time.1 The paper uses data from the OECD Fiscal Decentralisation database to calculate indicators related to property tax autonomy. In contrast to the spending power indicators, the tax autonomy indicator id available for many years and hence they have a time series dimension. This allows us to estimate our model for tax autonomy with a panel feature. In all the specifications the decentralisation indicators will be de-meaned by their cross-sectional average.

7.2.2. Model

This paper builds on the earlier work by Cavalleri, Cournède and Özsöğüt (2019[3]) who employ a stock-‑flow model of the housing market following the work of Wheaton and DiPasquale (1994[14]) to estimate the long-run relationship between the housing stock, prices and building costs. We build on the supply side equation of that model:

$S=I\left(P, X_1\right)+ {\left(1-\delta \right)S}_{t-1}\left(1\right)$

Equation 1 links the changes in the housing stock (S) to new investment (I) and changes in the value of the existing housing stock due to deprecation ($\delta )$. Housing investment (I) itself is a function of house prices (P) and building costs which are captured in vector $X_1$. In the emprical model we use real residential investment as a proxy for changes in the housing stock and a construction cost index to capture the costs of several construction inputs. The standard long-run model of Cavalleri, Cournède and Özsöğüt (2019[3]) is augmented by an interaction term between prices and the set of decentralisation indicators that are tested. This results in the following estimation model:

$Ln I_{ct}= {\beta }_c^0+{\beta }^{1}ln{P}_{ct} +{{\beta }^{2}Dec}_c+{\beta }^{3}ln{P}_{ct}*{Dec}_c{+{\beta }^{4}lnCC}_{ct}+h\text{'}{f}_t+{\epsilon }_{ct} \mathrm{ } \left(2\right)$

Where $I_{ct}\mathrm{ }$is real residential investment, $P_{ct}$ are real house prices and ${CC}_{ct}$ are construction costs for country c in quarter t. ${\beta }_1$ captures the long-run price elasticity of housing supply. This coefficient should be positive as higher prices should provide an incentive for developers to invest in housing. Coefficient ${\beta }_2$ controls for variation in the decentralisation (Dec) variable. Coefficient ${\beta }_3$ captures the interaction effect of our decentralisation variable. This tells us how much higher or lower the housing supply elasticity is given a certain degree of decentralisation. Because the decentralisation variables are all de-meaned, the supply elasticity for the average level of decentralisation is equal to ${\beta }_1$. For ${\beta }_4$ the coefficient is expected to be negative, since higher construction costs discourage housing investment for a given level of house prices. This specification captures long-term effects: for more detail on the short-term adjustment to the estimated long-term equilibrium, see Cavalleri, Cournède and Özsöğüt (2019[3]), and for a discussion of estimation strategies tailored to focussing on the short term, see Duca, Muellbauer and Murphy (2021[15]).

In the estimation for spending autonomy, the decentralisation indicators only appear in the interaction term, as its separate inclusion would result in perfect multicollinearity with the country fixed effects. However, in the estimation of the model for tax autonomy the decentralisation indicator also enters the model seperately as this variable has a panel feature.

The specification of equation (2) also deals with cross-sectional dependence, which comes from exogenous common forces that affect residential investment in all the countries in the panel. To do so, the long-run investment equation is estimated in a heterogeneous panel model with a general multi-factor structure using the common correlated coefficient approach first proposed by Pesaran (2006[16]). Vector f therefore consists of the cross-sectional averages of all the regressors and instruments that enter the model. These control for the unobserved common factors, which can for instance be global shocks (such as technological progress, synchronisation of housing cycles, global demographic trends) that affect residential investment differently in each country.

The estimation also needs to address potential endogeneity of residential investment and construction costs. Large increases in residential investment could, for instance, inflate construction costs. To tackle this potential bias, the estimation uses the lagged values of contruction costs as instruments. Furthermore, substantantial increases in housing supply following large increases in homebuilding could have an effect on house prices. To address this issue, the estimation uses the instrumentation strategy of Cavalleri, Cournède and Özsöğüt (2019[3]), augmented with the decentralisation variables. Total population and real disposable income per capita are instruments for prices where they are feasible and strong, which corresponds to 10 countries. The first and second lag of real house prices are used for the remaining 15 countries, since for these they better meet availability and validity criteria than population and income.

The instrumentation can be written as:

$Ln{P}_{ct}*{Dec}_c = {\beta }_c^0+{\beta }^1{Z}_{ct}^1+{\beta }^{2*}{Dec}_c+ {\beta }^3{Z}_{ct}^1*{Dec}_c +{\beta }^4{Z}_{ct}^2+{\beta }^5{Z}_{ct}^2*{Dec}_c+h_c\text{'}{f}_t+{\epsilon }_{ct}$ (3)

Z¹ and Z² represent the instruments and f is again a vector of cross-sectional means to account for cross-sectional dependence. Annex Table ‎7.A.2 provides the results of the standard unit roots and cointegration tests.

7.3. Empirical findings

Table ‎7.1 presents the results of the estimation of equation 2 using the dataset underpinning Cavalleri, Cournède and Özsöğüt (2019[3]) augmented with the spending autonomy indicator and its sub-components described in this paper. All the estimation results use the instrumental variables approach as outlined in section 7.2 and include cross-sectional means to correct for cross-sectional dependence (test results are shown in Annex Table ‎7.A.1). Column 1 of the table shows the baseline specification without an interaction term: it therefore yields the same overall supply elasticity as the pooled estimation in Cavalleri, Cournède and Özsöğüt (2019[3]). Because all variables are in logs, the coefficient on prices should be interpreted as an elasticity; hence a one per cent increase in house prices leads on average to a 0.96 per cent increase in real residential investment. The coefficient on construction costs is, however, not significant in the baseline estimation. Cavalleri, Cournède and Özsöğüt (2019[3]) show that mean group estimators or specifications with time fixed effects yield similar results with average supply elasticities close to unity.

Columns 2 to 6 show the estimations where house prices are interacted with the different components of the spending autonomy indicator (Phillips, 2020[4]). The estimation results show that the coefficients related to the interaction terms are negative and statistically significant. The autonomy measures used in columns 2-6 could be capturing the effects of land use availability and rental market regulation on housing supply elasticities as identified by Cavalleri, Cournède and Özsöğüt (2019[3]). However, the autonomy indicators are not correlated with the measures of land use governance and rental market regulation.

Since the variables are demeaned, the overall supply response can be calculated as the coefficient on real house prices plus the interaction term times the change in the policy indicator. For instance, a one-standard deviation increase in subnational government composite spending power (by 1.7 of the indicator value) is estimated to decrease the housing supply elasticity – or additional investment response – by about 40%. While this may be based on an unrealistically large policy shift, based on a full cross-country standard deviation, it nevertheless implies that large subnational spending autonomy could well make local governments much more vulnerable to lobbying from residents against new construction investment, in support of the literature on NIMBYism (Wassmer and Wahid, 2018[17]).

The spending autonomy indicators have a focus on decision-making concerning affordable housing. For commercial rental housing and owner-occupied housing, the distribution of responsibilities and power could in practice be different. As a robustness check, we therefore run the regression also on a smaller set of countries, for which there is also a spending power indicator available for housing more broadly. This indicator is taken from Dougherty and Philips (2019[13]), and is only available for a sub-set of countries in our panel data set. Annex Table ‎7.A.3 shows that the results are broadly similar to the results shown in Table ‎7.1. However, some dimensions of spending power do not yield significant results likely due to the smaller sample size, but may also reflect the importance of the affordable housing decision-making channel.

Table ‎7.1. Long-run elasticity interacted with spending power indicators

	Dependent Variable: Real residential investment
	(1)	(2)	(3)	(4)	(5)	(6)
Real house prices	0.956***	1.166***	1.116***	0.887***	1.153***	1.079***
	(0.105)	(0.111)	(0.126)	(0.126)	(0.121)	(0.119)
Lag of construction costs	-0.235	-0.563***	-0.489***	-0.217	-0.517***	-0.437**
	(0.147)	(0.169)	(0.178)	(0.170)	(0.175)	(0.171)
P x Spending power (Policy)		-0.367***
		(0.046)
P x Spending power (Budget)			-0.183***
			(0.019)
P x Spending power (Input)				-0.144***
				(0.022)
P x Spending power (Output)					-0.209***
					(0.024)
P x Spending power (Composite)						-0.233***
						(0.025)
Chi-squared	40502783***	15704684***	13489706***	24180855***	15778343***	16214490***
Countries	25	23	23	23	23	23
Observations	2,840	2,598	2,598	2,598	2,598	2,598
Adjusted R2	0.843	0.849	0.847	0.842	0.835	0.846

Note: Significance levels: *** p < .01, ** p < .05, * p < .1; Standard errors (in parentheses) are robust to arbitrary common correlated disturbances (Driscoll - Kraay).

Recent OECD work on spending authority in the health sector (Dougherty et al., 2021[18]) has shown that its effects on economic outcomes are not always linear. We therefore test for non-linear relationships by adding a quadratic interaction term to the previous specification (see Annex Table ‎7.A.4). The estimation results confirm the existence of non-linearities, but the sign of the estimated coefficients vary according to the various sub-components of spending power. In the regression, which considers the policy autonomy indicator, the coefficient of the quadratic term is negative (column 2), implying that its negative impact on the supply elasticity increases as housing policy decisions are more decentralised. In the regression that considers the input and budget autonomy indicator (column 3 and 4), the quadratic terms are positive. This implies that the negative effect of more decentralisation diminishes if budget and input autonomy increases. Lastly, the quadratic term related to the composite indicator (column 6) and the output indicator (column 5) is not significant.

Table ‎7.2 shows the estimation results for the specification with the property tax autonomy indicator. The results in column 2 suggest that more autonomy over property taxes should lead to a more elastic housing supply as local governments gain from allowing more housing construction. Again, since the variables are demeaned, the overall supply response can be calculated as the coefficient on real house prices plus the interaction term times the change in the policy indicator. For instance, a one-standard deviation increase in subnational property tax autonomy (by 0.25 of the value) is estimated to increase the housing supply elasticity, or the additional real housing investment response, by about 35%. While the tax and spending indicators are not directly comparable, the magnitude of this tax policy effect on the elasticity is roughly in line with a one-standard deviation increase in subnational spending power.

Table ‎7.2. Long-run elasticity interacted with the property tax autonomy indicator

	Dependent variable: Real residential investment
	(1)	(2)
Real house prices	0.956***	1.384***
	(0.105)	(0.135)
Lag of construction costs	-0.235	-0.723***
	(0.147)	(0.212)
P x Tax autonomy (Property taxes)		1.451***
		(0.472)
Tax autonomy (Property taxes)		-5.705***
		(1.852)
Chi-squared	40502783***	55404299***
Countries	25	24
Observations	2,840	2,653
R2	0.851	0.828
Adjusted R2	0.843	0.818

Note: Significance levels: *** p < .01, ** p < .05, * p < .1; Standard errors (in parentheses) are robust to arbitrary common correlated disturbances (Driscoll - Kraay).

7.4. Conclusion

This paper extends earlier work by Cavalleri, Cournède and Özsöğüt (2019[3]). It explores factors that could explain the large cross-country variation in housing supply elasticities. The present analysis examines the role of subnational governments in tax and spending decision-making regarding housing, by employing unique tax and spending autonomy indicators developed by the OECD Network on Fiscal Relations (Dougherty, Harding and Reschovsky, 2019[8]; Phillips, 2020[4]). The estimations suggest that countries where subnational governments have more spending authority in the area of housing, the responsiveness of the housing supply may be substantially lower (Figure ‎7.3, Panel A). This empirical finding supports the narrative of subnational government being more prone to the not-in-my-backyard phenomenon and lobbying by locals who oppose new development, if their influence on housing policymaking is larger. The results for housing supply are confirmed when we use an indicator that reflects policies related to affordable and housing more broadly. This is consistent with the recent debate around the possibility that democractic and equity objectives can come into conflict and influence the pace and scale of new local development (Scally and Tighe, 2015[19]).

Furthermore, this paper goes beyond the previous literature in looking at the degree of tax autonomy of state and local governments and the responsiveness of housing supply. The paper finds that a higher degree of subnational government autonomy over their tax base – in particular for property taxes, meaning they can levy a larger portion of these taxes – is associated with a significantly higher housing supply response (Figure ‎7.3, Panel B), which may help to overcome contrasting pressures, which could arise from unconditional spending decentralisation. This provides evidence for second generation fiscal federalism theory, which suggests that if local governments and their communities can benefit from new construction through increased property tax revenues – which may help to provide higher quality local public goods – they will be more inclined to allow new housing, helping to overcome potential community opposition.

Figure ‎7.3. Simulated effect of spending and property tax autonomy on housing supply elasticity

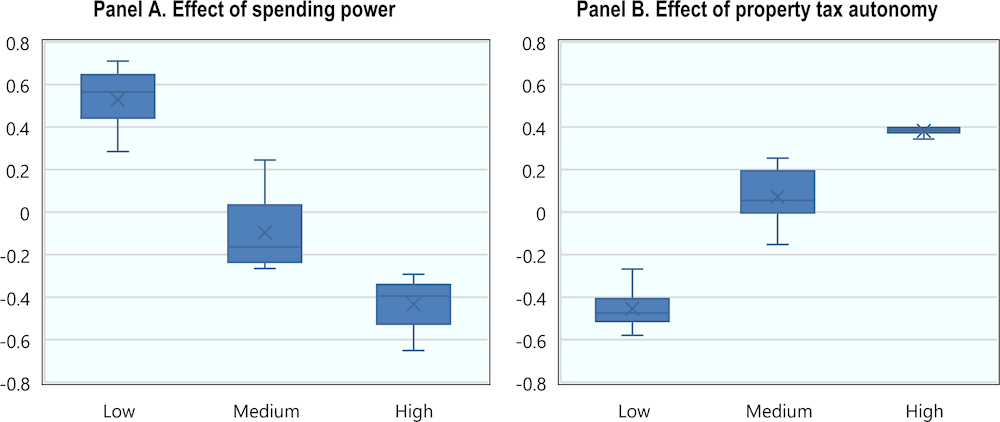
Note: Countries were divided into three equally-sized (Low/Medium/High) groups based on their spending power and property tax indicators. Then the marginal effects of the indicators on the housing supply elasticity are simulated using estimated country coefficients. The simulated effect of the spending power indicator is based on an elasticity of -0.233 for overall spending power on housing supply based on Table ‎7.1, while the effect of property tax autonomy is based on the 2018 indicators and an elasticity of 1.451 on housing supply elasticity based on Table ‎7.2.

Source: Authors’ calculations, with the help of ChatGPT4.

References

[12] Bétin, M. and V. Ziemann (2019), “How responsive are housing markets in the OECD? Regional level estimates”, OECD Economics Department Working Papers, No. 1590, OECD Publishing, Paris, https://doi.org/10.1787/1342258c-en.

[7] Blöchliger, H. et al. (2017), “Local taxation, land use regulation, and land use: A survey of the evidence”, OECD Economics Department Working Papers, No. 1375, OECD Publishing, Paris, https://doi.org/10.1787/52da7c6a-en.

[2] Caldera, A. and Å. Johansson (2013), “The price responsiveness of housing supply in OECD countries”, Journal of Housing Economics, Vol. 22/3, pp. 231-249.

[3] Cavalleri, M., B. Cournède and E. Özsöğüt (2019), “How responsive are housing markets in the OECD? National level estimates”, OECD Economics Department Working Papers, Vol. 1589, https://doi.org/10.1787/4777e29a-en.

[14] DiPasquale, D. and W. Wheaton (1994), “Housing Market Dynamics and the Future of Housing Prices”, Journal of Urban Economics, Vol. 35/1, pp. 1-27, https://doi.org/10.1006/juec.1994.1001.

[8] Dougherty, S., M. Harding and A. Reschovsky (2019), “Twenty years of tax autonomy across levels of government: Measurement and applications”, OECD Working Papers on Fiscal Federalism, No. 29, OECD Publishing, Paris, https://doi.org/10.1787/ca7ebc02-en.

[18] Dougherty, S. et al. (2021), “The impact of decentralisation on the performance of health care systems: a non-linear relationship”, The European Journal of Health Economics, Vol. 23/4, pp. 705-715, https://doi.org/10.1007/s10198-021-01390-1.

[13] Dougherty, S. and L. Phillips (2019), “The spending power of sub-national decision makers across five policy sectors”, OECD Working Papers on Fiscal Federalism, No. 25, OECD Publishing, Paris, https://doi.org/10.1787/8955021f-en.

[15] Duca, J., J. Muellbauer and A. Murphy (2021), “What Drives House Price Cycles? International Experience and Policy Issues”, Journal of Economic Literature, Vol. 59/3, pp. 773-864, https://doi.org/10.1257/jel.20201325.

[5] Fischel, W. (2004), The homevoter hypothesis : how home values influence local government taxation, school finance and land-use policies, Harvard University Press.

[11] Green, R., S. Malpezzi and S. Mayo (2005), “Metropolitan-Specific Estimates of the Price Elasticity of Supply of Housing, and Their Sources”, American Economic Review, Vol. 95/2, pp. 334-339.

[6] Hilber, C. and F. Robert-Nicoud (2013), “On the origins of land use regulations: Theory and evidence from US metro areas”, Journal of Urban Economics, Vol. 75, pp. 29-43.

[10] Hilber, C. and W. Vermeulen (2016), “The impact of supply constraints on house prices in England”, The Economic Journal, Vol. 126/591, pp. 358-405.

[1] OECD (2021), Brick by Brick: Building Better Housing Policies, OECD publishing Paris, https://doi.org/10.1787/b453b043-en.

[16] Pesaran, M. (2006), “Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure”, Econometrica, Vol. 74/4, pp. 967-1012.

[4] Phillips, L. (2020), “Decentralisation and Governance in the Housing Sector”, OECD Working Papers on Fiscal Federalism, Vol. 32.

[9] Saiz, A. (2010), “The Geographic Determinants of Housing Supply”, Quarterly Journal of Economics, Vol. 125/3, pp. 1253-1296.

[19] Scally, C. and J. Tighe (2015), “Democracy in Action?: NIMBY as Impediment to Equitable Affordable Housing Siting”, Housing Studies, Vol. 30/5, pp. 749-769, https://doi.org/10.1080/02673037.2015.1013093.

[17] Wassmer, R. and I. Wahid (2018), “Does the Likely Demographics of Affordable Housing Justify NIMBYism?”, Housing Policy Debate, Vol. 29/2, pp. 343-358, https://doi.org/10.1080/10511482.2018.1529694.

Annex 7.A. Robustness tests

Annex Table ‎7.A.1. Cross sectional dependence test results

Variable	CD Statistic	Mean ρ
Residential investment	58.97***	0.28
Real house prices	68.37***	0.34
Construction costs	64.27***	0.32
Total population	164.34***	0.77
Disposable income per capita	153.94***	0.77
∆ Residential investment	16.10	0.08
∆ Real house prices	25.85	0.13
∆ Construction costs	10.87	0.06
∆ Total population	9.22	0.04
∆ Disposable income per capita	13.08	0.07

Note: The test measures the mean correlation between panel units in individual variables. The panel dimension is 25 countries and the sample for the variables is 1980Q1 to 2017Q4. The null hypothesis is CS independence. The cross-sectional dependence measure (ρ) is the mean of the pair-wise correlation between the cross-section units of the variable. Pesaran (2006[16]) CD test for cross-sectional dependence in individual variables.

Source: Cavalleri, Cournède and Özsöğüt (2019[3]).

Annex Table ‎7.A.2. Panel unit root tests

Pesaran panel unit root test in the presence of cross-section dependence (CIPS test statistics)

Variable	Only intercept	With intercept and trend
Residential investment	-1.74	-2.87
Real house prices	-1.31	-1.87
Construction costs	-1.98	-1.95
Total population	-2.39	-2.33
Disposable income per capita	-2.01	-2.85
∆ Residential investment	-5.58	-5.71
∆ Real house prices	-4.38	-4.98
∆ Construction costs	-5.81	-6.03
∆ Total population	-0.69	-2.15
∆ Disposable income per capita	-6.10	-6.30

Note: Panel unit root tests for each variable, conducted over 25 countries and a horizon from 1980Q1 to 2017Q4. CIPS statistics are computed as the simple average of the individual specific CADF(2) tests, where two time lags are used in each regression. The null hypothesis is homogeneous non-stationarity, i.e., that all series have a unit root. The alternative hypothesis is that some series are stationary. Critical values for the CIPS statistics are -2.3, -2.16 and -2.08 for 1%, 5% and 10% significance, respectively, for the model with intercept only; -2.77, -2.65 and -2.59 for 1%, 5% and 10% significance, respectively, for the model with intercept and time trend.

Source: Cavalleri, Cournède and Özsöğüt (2019[3]).

Annex Table ‎7.A.3. Long-run elasticity interacted with general spending power indicators

	Dependent variable: Real residential investment
	(1)	(2)	(3)	(4)	(5)	(6)
Real house prices	0.956***	0.601**	0.891**	0.893***	0.869***	0.772***
	(0.105)	(0.237)	(0.396)	(0.233)	(0.120)	(0.132)
Lag of construction costs	-0.235	-0.069	-1.896	-0.258	0.131	0.166
	(0.147)	(0.380)	(1.490)	(0.367)	(0.267)	(0.275)
P x Spending power (Policy)		0.235
		(0.240)
P x Spending power (Budget)			2.122
			(1.546)
P x Spending power (Input)				-0.199***
				(0.067)
P x Spending power (Output)					-0.366***
					(0.081)
P x Spending power (Composite)						-0.535***
						(0.145)
Chi-squared	40502783***	241861***	84656***	174200***	148294***	166870***
Countries	25	11	11	11	11	11
Observations	2,840	1,303	1,303	1,303	1,303	1,303
Adjusted R2	0.843	0.850	0.433	0.847	0.844	0.839

Note: Significance levels: *** p < .01, ** p < .05, * p < .1; Standard errors (in parentheses) are robust to arbitrary common correlated disturbances (Driscoll - Kraay).

Annex Table ‎7.A.4. Long-run elasticity of housing supply interacted with quadratic spending power indicators

	Dependent variable: Real residential investment
	(1)	(2)	(3)	(4)	(5)	(6)
Real house prices	0.956***	1.426***	0.938***	0.638***	1.226***	1.074***
	(0.105)	(0.104)	(0.134)	(0.130)	(0.115)	(0.116)
Lag of construction costs	-0.235	-0.425**	-0.481***	-0.412**	-0.530***	-0.437**
	(0.147)	(0.175)	(0.176)	(0.168)	(0.167)	(0.175)
P x Spending power (Policy)		-0.239***
		(0.050)
P x Spending power (Policy)2		-0.241***
		(0.068)
P x Spending power (Budget)			-0.172***
			(0.018)
P x Spending power (Budget)2			0.030*
			(0.017)
P x Spending power (Input)				-0.075***
				(0.027)
P x Spending power (Input)2				0.051***
				(0.010)
P x Spending power (Output)					-0.204***
					(0.025)
P x Spending power (Output)2					-0.017
					(0.025)
P x Spending power (Composite)						-0.232***
						(0.026)
P x Spending power (Composite)2						0.002
						(0.035)
Chi-squared	40502783***	14684271***	19233289***	12784721***	14084937***	16453109***
Countries	25	23	23	23	23	23
Observations	2,840	2,598	2,598	2,598	2,598	2,598
R2	0.851	0.858	0.857	0.852	0.841	0.855
Adjusted R2	0.843	0.849	0.849	0.843	0.832	0.847

Note: Significance levels: ^*** p < .01, ^** p < .05, ^* p < .1; Standard errors (in parentheses) are robust to arbitrary common correlated disturbances (Driscoll - Kraay).

Note

← 1.  As a time-varying indicator would have been welcome for further econometric analysis, we explored whether local government shares in total housing expenditure could provide useable proxy measures of local government spending power. However, it turns out that such local government spending shares do not accurately reflect subnational spending power. For instance, local government spending can be high also in configurations where local authorities have a limited say over the expenditure (Phillips, 2020[4]). Quantitatively, these measures are only weakly correlated with each other.