Doris Zahner
Council for Aid to Education, United States
Tess Dawber
Council for Aid to Education, United States
Kelly Rotholz
Council for Aid to Education, United States
Does Higher Education Teach Students to Think Critically?
2. The Collegiate Learning Assessment – a performance-based assessment of generic skills
Abstract
Educators and employers clearly recognise that fact-based knowledge is no longer sufficient and that critical thinking, problem solving, and written communication skills are essential for success. The opportunity to improve students’ essential skills lies in identification and action. Assessments that provide educators with the opportunity to help students identify their strengths as well as areas where they can improve are fundamental to developing the critical thinkers, problem solvers and communicators who will be essential in the future. With close and careful attention paid toward students’ essential skills, even a small increase in the development of these skills could boost future outcomes for students, parents, institutions and the overall economy.
Introduction
The Collegiate Learning Assessment (CLA+) is an assessment of higher education students’ generic skills, specifically critical thinking, problem solving and written communication. These are skills and learning outcomes espoused by most higher education institutions (Association of American Colleges and Universities, 2011[1]; Arum and Roksa, 2011[2]; 2014[3]; Liu, Frankel and Roohr, 2014[4]; Wagner, 2010[5]), yet there is a lack of evidence on the extent to which improvement on them is actually achieved (Benjamin, 2008a[6]; 2008b[7]; 2012[8]; Bok, 2009[9]; Klein et al., 2007[10]).
A recent special report on higher education students’ career paths (Zinshteyn, 2021[11]) indicated the importance for institutions of higher education to acknowledge, understand and address the existing skills gap and mismatch and to prepare students for the world of work. This report echoes previous research (Montt, 2015[12])on the skills mismatch issue, which has been identified as globally problematic.
While content knowledge is a requisite part of a student’s education, alone it is insufficient for a student to thrive academically and professionally (Capital, 2016[13]; Hart Research Associates, 2013[14]; National Association of Colleges and Employers, 2018[15]; Rios et al., 2020[16]; World Economic Forum, 2016[17]). Most students (approximately 80%) consider themselves proficient in the essential college and career skills of critical thinking, problem solving and written communication. However, the percentage of employers who rate recent graduates as proficient in these skills differs greatly: 56% for critical thinking/problem solving and 42% for communication (National Association of Colleges and Employers, 2018[15]).
Specifically, essential college and career skills such as critical thinking, problem solving and communication are the abilities that hiring managers value most (Capital, 2016[13]; Hart Research Associates, 2013[14]; National Association of Colleges and Employers, 2018[15]; Rios et al., 2020[16]; World Economic Forum, 2016[17]). More than content knowledge, these are the skills that can help students entering higher education achieve better outcomes, such as a higher cumulative GPA during their college tenure (Zahner, Ramsaran and Zahner, 2012[18]). However, these essential skills are often not explicitly taught as part of college curricula, nor are they reflected on a college transcript.
The Council for Aid to Education’s (CAE) research shows that approximately 60% of entering students are not proficient in these skills, and since these skills are seldom explicitly taught as part of college curricula, most students have little structured opportunity to improve their proficiency. Identifying and supporting students who may be at risk due to insufficient proficiency in these essential skills upon entry to higher education should be one component to helping improve persistence, retention, and graduation rates. Improving students’ essential skills in secondary education to better prepare them for higher education should be another important component. Measuring these essential skills can be best accomplished by using an authentic, valid, and reliable assessment.
Educators and employers clearly recognise that fact-based knowledge is no longer sufficient and that critical thinking, problem solving, and written communication skills are essential for success. The opportunity to improve students’ essential skills lies in identification and action. Assessments that provide educators with the opportunity to help students identify their strengths as well as areas where they can improve are fundamental to developing the critical thinkers, problem solvers and communicators who will be essential in the future. With close and careful attention paid toward students’ essential skills, even a small increase in the development of these skills could boost future outcomes for students, parents, institutions and the overall economy.
CLA+
The Collegiate Learning Assessment (CLA /CLA+) is a performance-based assessment of critical thinking and written communication. Traditionally, the CLA was an institutional-level assessment that measured student learning gains within a university (Klein et al., 2007[10]). The CLA employed a matrix sampling approach under which students were randomly distributed either a Performance Task (PT) or an Analytic Writing Task for which students were allotted 90 minutes and 75 minutes, respectively. The CLA PTs presented real-world situations in which an issue, problem or conflict was identified and students were asked to assume a relevant role to address the issue, suggest a solution or recommend a course of action based on the information provided in a document library. Analytic Writing Tasks consisted of two components – one in which students were presented with a statement around which they had to construct an argument (Make an Argument), and another in which students were given a logically flawed argument that they had to then critique (Critique an Argument).
In its original form, the utility of the CLA was limited. Because the assessment consisted of just one or two responses from each student, reliable results were only available at the institutional level, and students’ results were not directly comparable. Likewise, reporting for the CLA was restricted to the purposes of its value-added measure, and institutions were not eligible for summary results unless they had tested specified class levels in the appropriate testing windows.
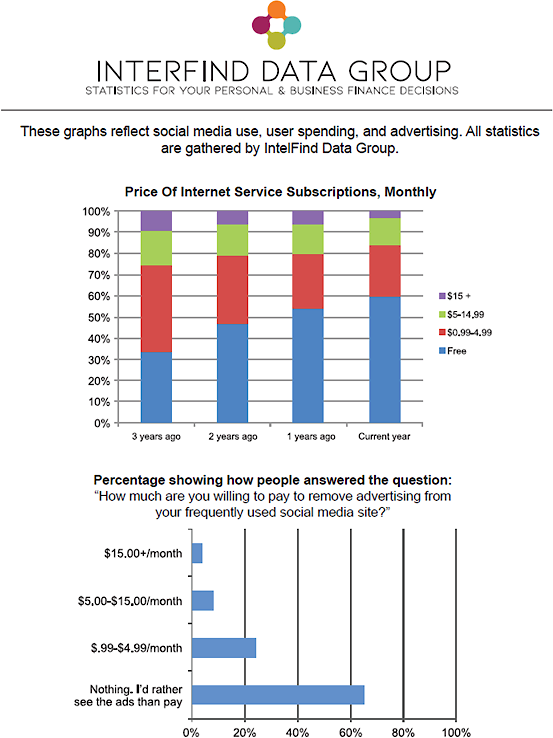
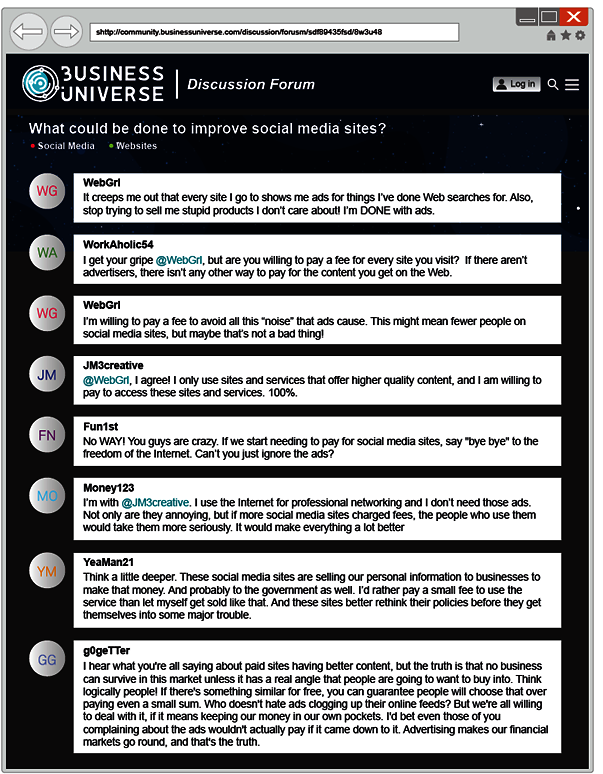
Thus, the CLA+ was created with a PT similar to the original CLA PT as the anchor of the assessment. The CLA+ also includes an additional set of 25 selected-response questions (SRQs) to increase the reliability of the instrument (Zahner, 2013[19]) for reporting individual student results. The SRQ section is aligned to the same construct as the PT and is intended to assess higher-order cognitive skills rather than the recall of factual knowledge. Similar to the PT, this section presents students with a set of questions as well as one or two documents to refer to when answering each question. The supporting documents include a range of information sources such as letters, memos, photographs, charts, and newspaper articles. Each student receives both components (PT and SRQ) of the assessment.
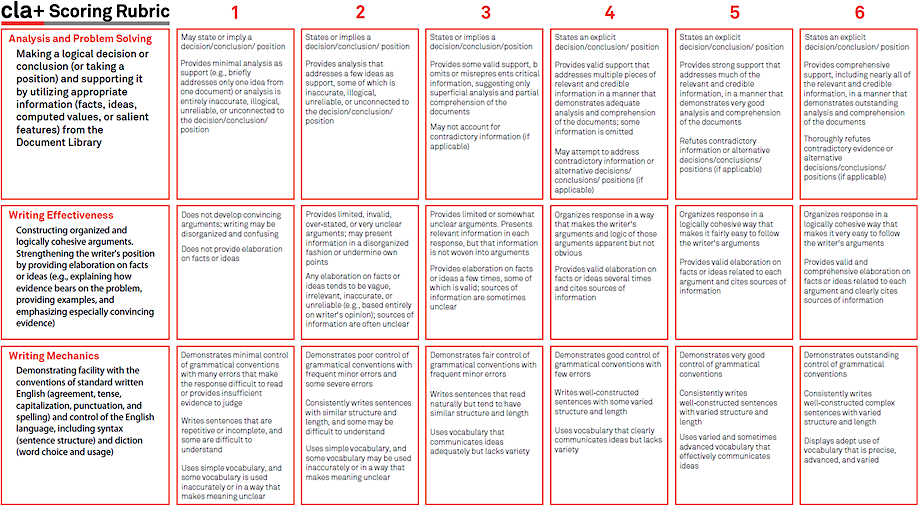
The CLA+ has six separate subscores. The open-ended student responses from the PT are scored on three subscores, which have a range from 1 – 6: Analysis and Problem Solving (APS), Writing Effectiveness (WE) and Writing Mechanics (WM). The SRQs consist of three subsections: Scientific and Quantitative Reasoning (SQR), Critical Reading and Evaluation (CRE) and Critiquing an Argument (CA). Students have 60 minutes to complete the PT and 30 minutes to complete the SRQs. There is a short demographic survey following the assessment, which should be completed within 15 minutes.
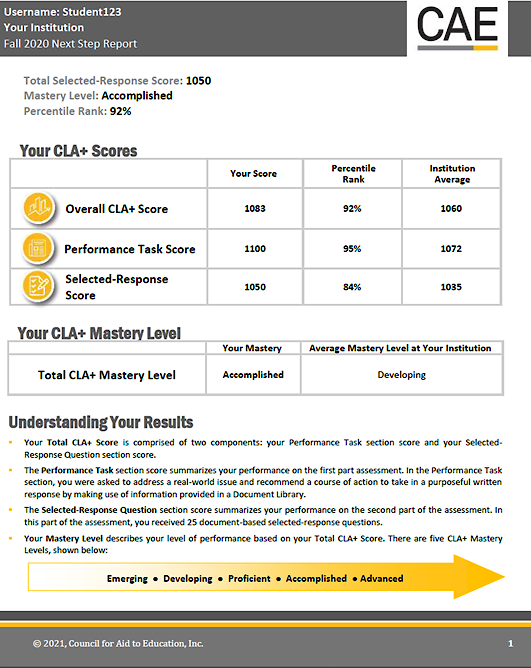
Additionally, CLA+ includes a metric in the form of mastery levels. The mastery levels are qualitative categorisations of total CLA+ scores, with cut scores that were derived from a standard-setting study (Zahner, 2014[20]). The mastery level categories are: Emerging, Developing, Proficient, Accomplished and Advanced.
Sample CLA+ documents can be found at the end of this chapter. These include PT and SRQ documents and questions, the scoring rubric, a sample institutional report and a sample student report.
CLA+ Scoring
All student PT responses are double-scored, one by an AI scoring engine, and the other by a trained human scorer.
Scoring process
For CLA+, all student responses are double-scored, once by a human rater and once through an AI scoring engine. The training for the scoring process is directed by the CAE Measurement Science team. All scorer candidates are selected for their experience with teaching and grading university student writing and have at least a master’s degree in an appropriate subject (e.g., English). Once selected, to become a CLA+ scorer, they must undergo rigorous training aligned with best practices in assessment.
A lead scorer is identified for each PT and is trained in person or virtually by CAE measurement scientists and editors. Following this training, the lead scorer conducts an in-person or virtual (but synchronous) training session for the scorers assigned to his or her particular PT. A CAE measurement scientist or editor attends this training as an observer and mentor. After this training session, homework assignments are given to the scorers in order to calibrate the entire scoring team. All training includes an orientation to the prompt and scoring rubrics/guides, repeated practice grading a wide range of student responses, and extensive feedback and discussion after scoring each response. Because each prompt may have differing possible arguments or relevant information, scorers receive prompt-specific guidance in addition to the scoring rubrics. CAE provides a scoring homework assignment for any PT that will be operational before the onset of each testing window to ensure that the scorers are properly calibrated. For new Performance Tasks (i.e. pilot testing), a separate training is first held to orient a lead scorer to the new PT, and then a general scorer training is held to introduce the new PT to the scorers. After participating in training, scorers complete a reliability check where they score the same set of student responses. Scorers with low agreement or reliability (determined by comparisons of raw score means, standard deviations, and correlations among the scorers) are either further coached or removed from scoring.
During pilot testing of any new PTs, all responses are double-scored by human scorers. These double-scored responses are then used for future scorer trainings, as well as to train a machine-scoring engine for all future operational test administrations of the PT.
Until 2020, CAE used Intelligent Essay Assessor (IEA) for its machine scoring. IEA is the automated scoring engine developed by Pearson Knowledge Technologies to evaluate the meaning of a text, not just writing mechanics. Pearson designed IEA for CLA+ using a broad range of real CLA+ responses and scores to ensure its consistency with scores generated by human scorers. Thus, human scorers remain the basis for scoring the CLA+ tasks. However, automated scoring helps to increase scoring accuracy, reduce the amount of time between a test administration and reports delivery, and lower costs. The automated essay scoring technique that CLA+ uses is known as Latent Semantic Analysis (LSA), which extracts the underlying meaning in written text. LSA uses mathematical analysis of at least 800 student responses per PT and the collective expertise of human scorers (each of these responses must be accompanied by two sets of scores from trained human scorers), and applies what it has learned from the expert scorers to new, unscored student responses. Beginning in 2021, CAE engaged a new partner, MZD for delivery and scoring of PTs. MZD’s platform has an integrated automatic scoring engine, EMMA (Powers, Loring and Henrich, 2019[21])which functions very similarly to IEA. In fact, CAE conducted a comparison of the two AI-scoring platforms and found the results between EMMA and IEA to be comparable.
Once tasks are fully operational, CLA+ uses a combination of automated and human scoring for its Performance Tasks. In almost all cases, IEA provides one set of scores and a human provides the second set. However, IEA occasionally identifies unusual responses. When this happens, the flagged response is automatically sent to the human scoring queue to be scored by a second human instead of by IEA. For any given response, the final PT subscores are simply the averages of the two sets of scores, whether one human set and one machine set or two human sets.
To ensure continuous human scorer calibration, CAE developed the calibration system for the online scoring interface. The calibration system was developed to improve and streamline scoring. Calibration of scorers through the online system requires scorers to score previously scored results, or “verification papers,” when they first start scoring, as well as throughout the scoring window. The system will periodically present verification papers to scorers in lieu of student responses, though they are not flagged to the scorers as such. The system does not indicate when a scorer has successfully scored a verification paper; however, if the scorer fails to accurately score a series of verification papers, he or she will be removed from scoring and must participate in a remediation process. At this point, scorers are either further coached or removed from scoring.
Using data from the CLA, CAE used an array of Performance Tasks to compare the accuracy of human versus automated scoring. For all tasks examined, AI engine-scores agreed more often with the average of multiple experts (r = .84-.93) than two experts agreed with each other (r = .80-.88). These results suggest that computer-assisted scoring is as accurate as–and in some cases, more accurate than–expert human scorers (Steedle and Elliot, 2012[22]).
CLA+ psychometrics
Test design
The test design of the CLA+ assessment is shown in Table 2.1. The numbers of items and points are given for both test components and for the total test. The three SRQ subscores – SQR, CRE, and CA – are reporting categories that consist of items measuring a similar set of skills.
Student responses to the PT are scored with three rubrics, each scored from 1 to 6. The subscores given for the PTs are APS, WE, and WM.
Table 2.1. CLA+ test design
Note: SQR = Scientific and Quantitative Reasoning; CRE = Critical Reading and Evaluation; CA = Critique an Argument; APS = Analysis and Problem Solving; WE = Writing Effectiveness; WM = Writing Mechanics.
CAE uses a matrix sampling design. Multiple SRQ sets and PTs are randomly spiralled across the students during a given administration. As a result, the reliability analyses are performed by subscore for the SRQ sets and by PTs rather than by form. The data summarised below are based on the CLA+ administrations with domestic students.
Reliability
Reliability refers to the consistency of students’ test scores on parallel forms of a test. A reliable test is one that produces relatively stable scores if the test is administered repeatedly under similar conditions. Reliability was evaluated using the method of internal consistency, which provides an estimate of how consistently examinees perform across items within a test during a single test administration (Crocker and Algina, 1986[23]).
The reliability of raw scores was estimated using Cronbach’s coefficient alpha, which is a lower-bound estimate of test reliability (Cronbach, 1951[24]). Reliability coefficients range from 0 to 1, where 1 indicates a perfectly reliable test. Generally, a longer test is expected to be more reliable than a shorter test.
Because the PT scores consist of ratings rather than sets of items, the reliability of the ratings is summarised by rater consistency indices. These are rater agreement and correlations between rater scores.
SRQ reliability
The average internal consistency results for the SRQ sets available for operational use are 0.58 for the SQR, 0.59 for the CRE and 0.48 for the CA. The reliabilities are higher for the two ten-item sets compared to the five-item set.
PT reliability
The rater consistency is summarised for exact agreement and exact plus adjacent agreement on ratings, and for correlations between rater scores for the APS, WE and WM ratings. Across PTs and administrations, the exact agreement rates for the three ratings are between 59 and 61 percent and the exact plus adjacent agreement rates are 97 percent or higher. Correlations between rater scores are in the 0.60 to 0.70 range.
Correlations between scale scores
The correlations between the CLA+ total scale score and the component scale scores (i.e. PT, SRQ) are in the 0.80 to 0.90 range. The correlations between the PT and the SRQ scale scores generally are between 0.40 and 0.50. The correlations between the PT and the SRQ subscores of SQR, CRE and CA tend to be between 0.30 and 0.40 for SQR and CRE (both ten-point sets) and between 0.25 and 0.40 for CA (five-point set).
Computing scale scores
SRQ subscores are assigned based on the number of questions answered correctly. The value is adjusted to account for item difficulty, and the adjusted value is converted to a common scale. The scale has a mean of 500 and a standard deviation of 100. SRQ subscores range from approximately 200 to 800. The weighted average of the SRQ subscores is transformed using the scaling parameters to place the SRQ section scores on the same scale.
PT subscores are assigned on a scale of 1 to 6 according to the scoring rubric. The PT subscores are not adjusted for difficulty because they are intended to facilitate criterion-referenced interpretations outlined in the rubric. The PT subscores are added to produce a total raw score, which is then converted to a common scale using linear transformation. The conversion produces scale scores that maintain comparable levels of performance across PTs.
The CLA+ total scores are calculated by taking the average of the SRQ and the PT scale scores. The mastery level cut scores are applied to the CLA+ total score to assign mastery levels to the student scores.
Technical information about the linear equating procedure (Kolen and Brennan, 2004[25]) is provided in the Annex to this chapter.
Establishing mastery levels
The total test scale scores are contextualised by assigning mastery, or performance, levels. A standard-setting workshop was held in December 2013 to set the performance standards for Developing, Proficient and Advanced. A fourth performance standard, Accomplished, was added in November 2014 using the same methodology and panellists.
Panellist discussions were based on the knowledge, skills and abilities required to perform well on the CLA+. The purpose of the activity was to develop consensus among the panellists regarding a narrative profile of the knowledge, skills and abilities required to perform at each mastery level. Then, during the rating activities, panellists relied on these descriptions to make their judgments based on the items and student performance. Table 2.2 shows the CLA+ cut scores used to assign mastery levels.
Table 2.2. CLA+ mastery level cut scores
Figure 2.1. Sample CLA+ PT
Figure 2.2. Document 1: Penpals Draft Business Plan
Figure 2.3. Document 2: Memo from Nelson Fareira. J.D.
Figure 2.4. Document 3: Statistics on Internet Apps and Internet Ads.
Figure 2.5. Document 4: Business Universe Online Discussion Forum
Figure 2.6. Document 5: Article from Bottom Line Magazine
Figure 2.7. Document 6: Email from Imani Willis, ReCrucial Recruriting Website
Figure 2.8. Sample CLA+ SRQ (Part 1)
Figure 2.9. Sample CLA+ SRQ (Part 2)
Figure 2.10. Sample CLA+ SRQ (Part 3)
Figure 2.11. CLA+ scoring rubric
Figure 2.12. Sample CLA+ institutional report
Figure 2.13. Sample CLA+ student report
References
[3] Arum, R. and J. Roksa (2014), Aspiring Adults Adrift. Tentative Transitions of College Graduates, Chicago University Press, Chicago, IL.
[2] Arum, R. and J. Roksa (2011), Academically Adrift. Limited Learning on College Campuses, Chicago University Press, Chicago, IL.
[1] Association of American Colleges and Universities (2011), “The LEAP Vision for Learning: Outcomes, Practices, Impact, and Employers’ Views”, Vol. 26/3, p. 34.
[8] Benjamin, R. (2012), “The Seven Red Herrings About Standardized Assessments in Higher Education”, National Institute for Learning Outcomes Assessment September, pp. 7-14.
[6] Benjamin, R. (2008a), “The Case for Comparative Institutional Assessment of Higher-Order Thinking Skills”, Change: The Magazine of Higher Learning, Vol. 40/6, pp. 50-55, https://doi.org/10.3200/chng.40.6.50-55.
[7] Benjamin, R. (2008b), The Contribution of the Collegiate Learning Assessment to Teaching and Learning, Council for Aid to Education, New York.
[9] Bok, D. (2009), Our Underachieving Colleges: A Candid Look at How Much Students Learn and Why They Should Be Learning More, https://doi.org/10.1111/j.1540-5931.2007.00471.x.
[13] Capital, P. (2016), 2016 Workforce-Skills Preparedness Report, http://www.payscale.com/data-packages/job-skills.
[23] Crocker, L. and J. Algina (1986), Introduction to Classical and Modern Test Theory, Wadsworth Group/Thomson Learning, Belmont, CA.
[24] Cronbach, L. (1951), “Coefficient alpha and the internal structure of tests”, Psychometrika, Vol. 16/3, pp. 297-334, https://doi.org/10.1007/BF02310555.
[14] Hart Research Associates (2013), “It takes more than a major: Employer priorities for college learning and student success”, Liberal Education, Vol. 99/2.
[10] Klein, S. et al. (2007), “The collegiate learning assessment: Facts and fantasies”, Evaluation Review, Vol. 31/5, pp. 415-439, https://doi.org/10.1177/0193841X07303318.
[25] Kolen, M. and R. Brennan (2004), Test Equating, Scaling, and Linking: Methods and Practices, 2nd Ed., Springer, New York.
[4] Liu, O., L. Frankel and K. Roohr (2014), “Assessing Critical Thinking in Higher Education: Current State and Directions for Next-Generation Assessment”, ETS Research Report Series, Vol. 2014/1, pp. 1-14, https://doi.org/10.1002/ets2.12009.
[12] Montt, G. (2015), “The causes and consequences of field-of-study mismatch: An analysis using PIAAC”, OECD Social, Employment & Migration Working Papers 167.
[15] National Association of Colleges and Employers (2018), Are college graduates “career ready”?, https://www.naceweb.org/career-readiness/competencies/are-college-graduates-career-ready/ (accessed on 19 February 2018).
[21] Powers, S., M. Loring and Z. Henrich (2019), Essay Machine Marking Automation (EMMA) Research Report, MZD.
[16] Rios, J. et al. (2020), “Identifying Critical 21st-Century Skills for Workplace Success: A Content Analysis of Job Advertisements”, Educational Researcher, Vol. 49/2, pp. 80-89, https://doi.org/10.3102/0013189X19890600.
[22] Steedle, J. and S. Elliot (2012), The efficacy of automated essay scoring for evaluating student responses to complex critical thinking performance tasks, Council for Aid to Education, New York, NY.
[5] Wagner, T. (2010), The Global Achievement Gap: Why Even Our Best Schools Don’t Teach the New Survival Skills Our Children Need – and What We Can Do about It, Basic Books, New York, NY.
[17] World Economic Forum (2016), Global Challenge Insight Report: The Future of Jobs: Employment, Skills and Workforce Strategy for the Fourth Industrial Revolution, World Economic Forum, http://www3.weforum.org/docs/WEF_Future_of_Jobs.pdf.
[20] Zahner, D. (2014), CLA+ Standard Setting Study Final Report, Council for Aid to Education, New York, NY.
[19] Zahner, D. (2013), Reliability and Validity – CLA+, Council for Aid to Education, New York, NY.
[18] Zahner, D., L. Ramsaran and D. Zahner (2012), “Comparing alternatives in the prediction of college success”, Annual Meeting of the American Educational Research Association.
[11] Zinshteyn, M. (2021), “Careers in a Changing Era: How Higher Ed Can Fight the Skills Gap and Prepare Students for a Dynamic World of Work”, Inside Higher Ed..
Annex 2.A. Linear equating procedure
CAE uses linear equating to transform the scores to the reporting scale. The following technical information is obtained from Kolen and Brennan (2004[25]).
In linear equating, scores that are equal distance from their means in standard deviation units are set to be equal. Linear equating can be viewed as allowing for the scale units, as well as the means, of the two forms to differ.
Define as the mean on Form X and μ(Y) as the mean on Form Y for a population of examinees.
Define as the standard deviation of Form X and σ(Y) as the standard deviation of Form Y.
The linear conversion is defined by setting standardised deviation scores (z-scores) on the two forms to be equal such that:
One way to express the linear equation for converting observed scores on Form X to the scale of Form Y is the following:
The expression is a linear equation of the form slope (x) + intercept with:
, and
The CLA+ equating procedures are described below.
The SRQ raw subscores (SQR, CRE, CA) undergo a scaling process to correct for different levels of difficulty of the subscore sections. The scaled mean and standard deviation for each subscore are approximately 500 and 100, respectively. The SRQ total score is computed by taking a weighted average of the SRQ subscores, with weights corresponding to the number of items of each subscore section. The SRQ total score then undergoes a linear transformation to equate it to the scores obtained by our norm population of college freshmen on the original set of SRQs. This process ensures that SRQ scores can be compared with one another regardless of which SRQ set was administered or in which year the test was taken.
The PT raw subscores are summed to produce a single raw PT total score. The raw PT total score undergoes a linear transformation to equate it to the scores obtained by our norm population of college freshmen on the original set of PTs. This ensures that PT scores can be compared with one another regardless of which PT was administered or in which year the test was taken. The CLA+ total scale score is computed by averaging the SRQ and PT scale scores. All three scale scores (SRQ, PT, total) range from 400 to 1 600, the normal SAT Math and Critical Reading score scale.
Because the CLA+ is administered in different languages, separate scalings are performed based on language of administration. For example, the linear transformations applied for the Spanish tests administered in Mexico and Chile were the same for a given SRQ set or PT, as were the linear transformations applied for the English tests administered in the US and the UK.