This chapter compares students’ mean scores and the variation in their performance in mathematics, reading and science across the countries and economies that participated in the PISA 2022 assessment.
PISA 2022 Results (Volume I)

2. How did countries perform in PISA?
Abstract
For Netherlands, Newfoundland and Labrador, Alberta, Hong Kong (China), Manitoba, United States, Latvia, Scotland, Quebec, New Zealand, United Kingdom, Northern Ireland, England, Wales, Denmark, Ontario, Panama, Nova Scotia, Australia, British Columbia, Ireland, Jamaica and Canada, caution is required when interpreting estimates because one or more PISA sampling standards were not met (see Reader’s Guide, Annexes A2 and A4).
What the data tell us
Singapore scored significantly higher, on average, than all other countries and economies that participated in PISA 2022 in mathematics (575 points), reading (543 points) and science (561 points).
In mathematics, six East Asian education systems (Hong Kong [China]*, Japan, Korea, Macao [China], Singapore and Chinese Taipei) outperformed all other countries and economies. In reading, behind top-performing education system Singapore, Ireland* performed as well as Estonia, Japan, Korea and Chinese Taipei and better than 75 other countries and economies. In science, the highest performing countries are the same six East Asian countries/economies, Canada* and Estonia.
The gap in performance between the highest- and lowest-performing countries is 153 score points in mathematics among OECD countries and 238 points among all education systems that took part in PISA 2022.
The gap between the 90th percentile of mathematics performance (the score above which only 10% of students scored) and the 10th percentile of performance (the score below which only 10% of students scored) is more than 135 score points in all countries and economies. On average across OECD countries, 235 score points separate these extremes.
PISA measures student performance as the extent to which 15-year-old students near the end of their compulsory education have acquired the knowledge and skills that are essential for full participation in modern societies, particularly in the core domains of reading, mathematics, and science.
This chapter examines student performance in PISA 2022. In its first section, the chapter reports the average performance in mathematics, reading and science for each country and economy, comparing it to other countries and economies, and to the average performance across OECD countries. The second section examines variation in performance within and between countries and economies; for example, it shows how large the score gap that separates the highest-performing and lowest-performing students within each country and economy is. It also examines how variation in performance is related to the average performance across PISA-participating countries and economies. A student performance ranking among all countries and economies that took part in PISA 2022 is provided in the third section.
Trends in student performance over time are considered in Chapters 5 and 6 of this report. For short-term changes between PISA 2018 and 2022, see Chapter 5; for long-term trajectories in student performance over countries’ entire participation in PISA, see Chapter 6.
Average performance in mathematics, reading and science
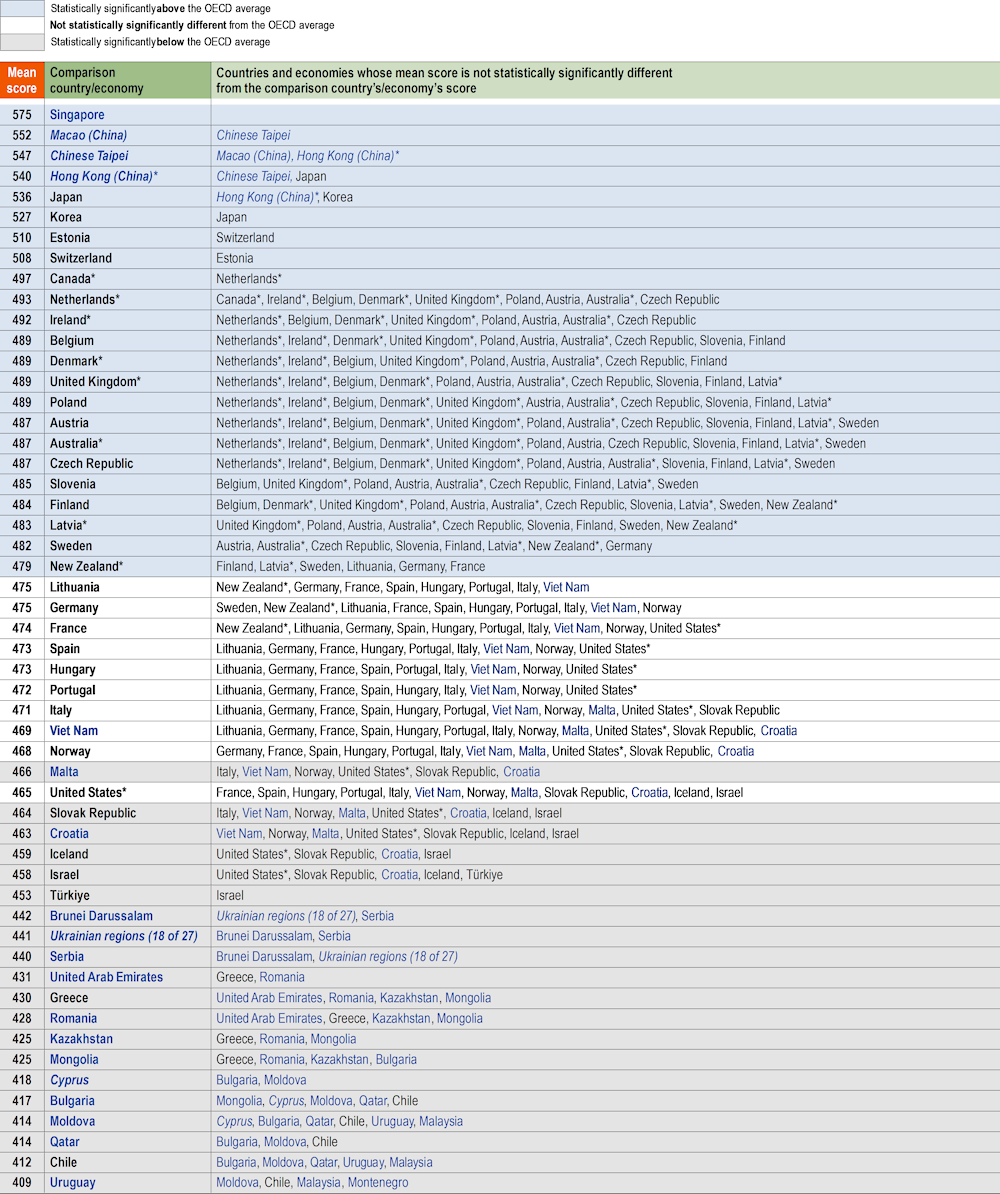
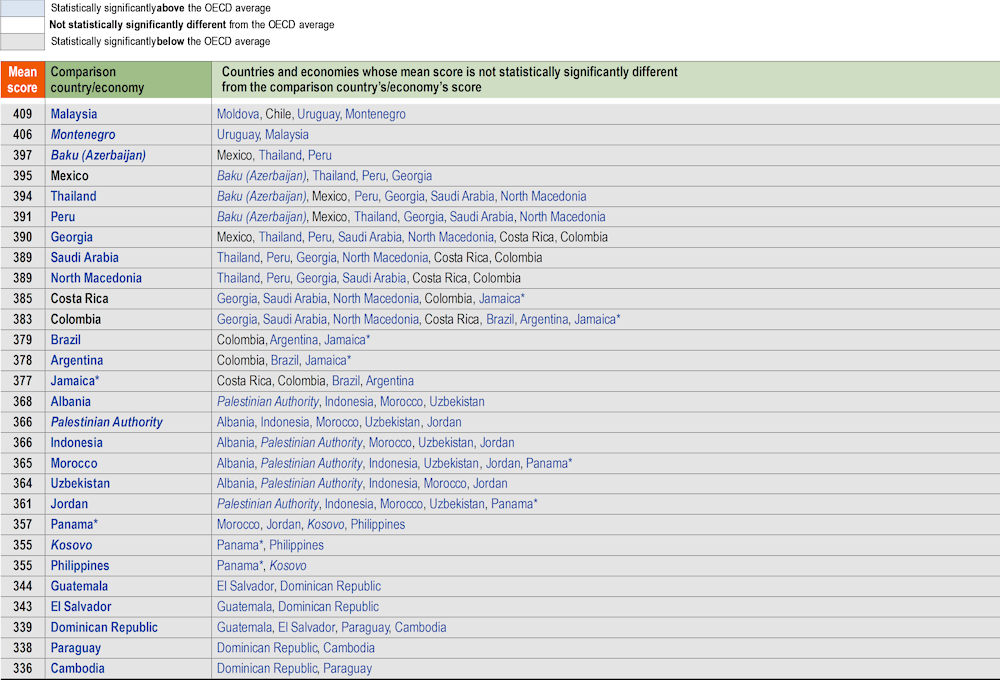
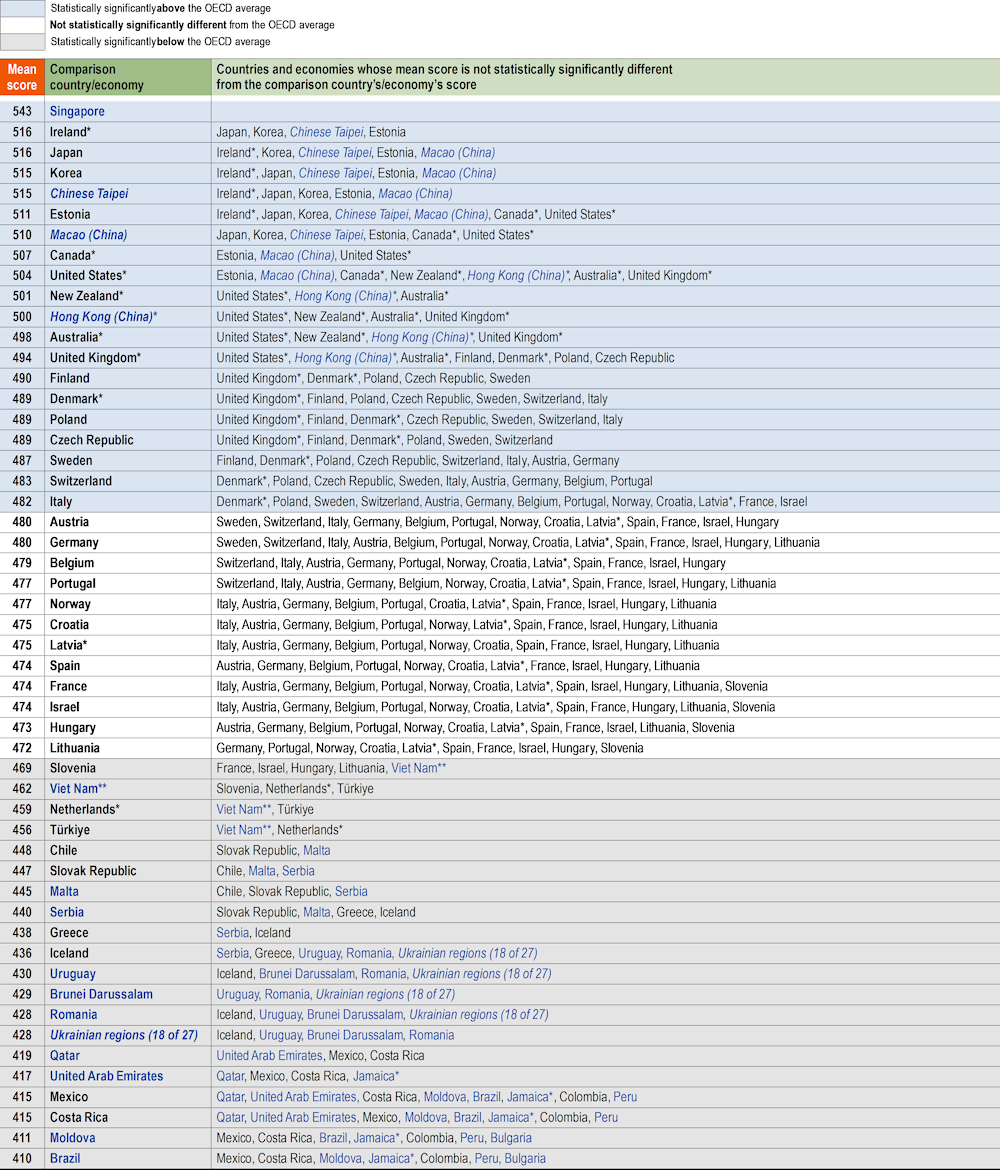
In PISA 2022, the mean mathematics score among OECD countries is 472 points; the mean score in reading is 476 points; and the mean score in science is 485 points. Singapore scored significantly higher than all other countries/economies that participated in PISA 2022 in mathematics (575 points), reading (543 points) and science (561 points).
Table I.2.1, Table I.2.2 and Table I.2.3 show each country’s/economy’s mean score and indicate pairs of countries/economies where the differences between the means are statistically significant1. For each country/economy shown in the middle column, the countries/economies whose mean scores are not statistically significantly different are listed in the right column. In these tables, countries and economies are divided into three broad groups: those whose mean scores are statistically around the OECD mean (highlighted in light grey); those whose mean scores are above the OECD mean (highlighted in blue); and those whose mean scores are below the OECD mean (highlighted in dark grey).
In mathematics, six East Asian education systems (Hong Kong [China]*, Japan, Korea, Macao [China], Singapore and Chinese Taipei) outperformed all other countries and economies (Table I.2.1). Another 17 countries also performed above the OECD average in mathematics, ranging from Estonia (mean score of 510 points) to New Zealand* (mean score of 479 points).
In reading, behind the top-performing education system (Singapore), Ireland* performed as well as Estonia, Japan, Korea and Chinese Taipei; and outperformed all other countries/economies (Table I.2.1). In addition to those six countries and economies, another 14 education systems performed above the OECD average in reading, ranging from Macao (China) (mean score of 510) to Italy (mean score of 482 points).
All countries and economies that performed above the OECD average in mathematics also performed above the OECD average in reading, except for Austria, Belgium, Latvia*, the Netherlands* and Slovenia. Similarly, all countries and economies that performed above the OECD average in reading also performed above the OECD average in mathematics, except for Italy and the United States*.
In science, the highest-performing education systems are Canada*, Estonia, Hong Kong (China)*, Japan, Korea, Macao (China), Singapore and Chinese Taipei (Table I.2.2). Finland performed as well as Canada* in science. In addition to these nine countries and economies, another 15 education systems also performed above the OECD average in science, ranging from Australia* (mean score of 507 points) to Belgium (mean score of 491 points).
All countries and economies that performed above the OECD average in science also performed above the OECD average in mathematics and reading, except for six countries/economies. Austria, Belgium, Latvia* and Slovenia performed above the OECD average in science and mathematics but not in reading; United States performed above the OECD average in science and reading but not in mathematics; and Germany performed above the OECD average in science but not in mathematics or reading. In both of these subjects, Germany’s mean score is not statistically significantly different from the OECD average.
Eighteen countries and economies performed above the OECD average in mathematics, reading and science (Australia*, Canada*, the Czech Republic, Denmark*, Estonia, Finland, Hong Kong [China]*, Ireland*, Japan, Korea, Macao [China], New Zealand*, Poland, Singapore, Sweden, Switzerland, Chinese Taipei and the United Kingdom*).
The gap in performance between the highest- and lowest-performing countries is 153 score points in mathematics among OECD countries and 238 points among all education systems that took part in PISA 2022. In reading, the gap in performance between the highest- and lowest-performing countries is 107 score points among OECD countries and 214 points among all education systems that took part in PISA 2022. In science, the gap in performance between the highest- and lowest-performing countries is 137 score points among OECD countries and 214 points among all education systems that took part in PISA 2022.
Table I.2.1. Comparing countries’ and economies’ performance in mathematics [1/2]
Countries and economies are ranked in descending order of the mean performance in mathematics.
Source: OECD, PISA 2022 Database, Table I.B1.2.1.
Table I.2.1. Comparing countries’ and economies’ performance in mathematics [2/2]
Countries and economies are ranked in descending order of the mean performance in mathematics.
Source: OECD, PISA 2022 Database, Table I.B1.2.1.
Table I.2.2. Comparing countries’ and economies’ performance in reading [1/2]
** Caution is required when comparing estimates based on PISA 2022 with other countries/economies as a strong linkage to the international PISA reading scale could not be established (see Reader's Guide and Annex A4).
Countries and economies are ranked in descending order of the mean performance in reading.
Source: OECD, PISA 2022 Database, Table I.B1.2.2.
Table I.2.2. Comparing countries’ and economies’ performance in reading [2/2]
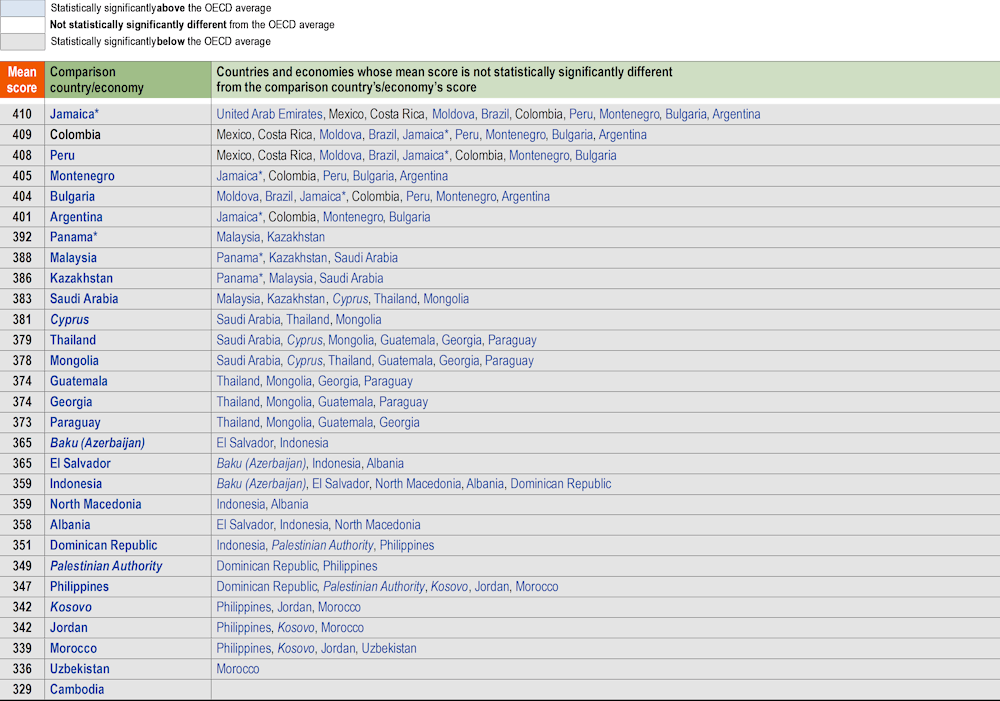
** Caution is required when comparing estimates based on PISA 2022 with other countries/economies as a strong linkage to the international PISA reading scale could not be established (see Reader's Guide and Annex A4).
Countries and economies are ranked in descending order of the mean performance in reading.
Source: OECD, PISA 2022 Database, Table I.B1.2.2.
Table I.2.3. Comparing countries’ and economies’ performance in science [1/2]
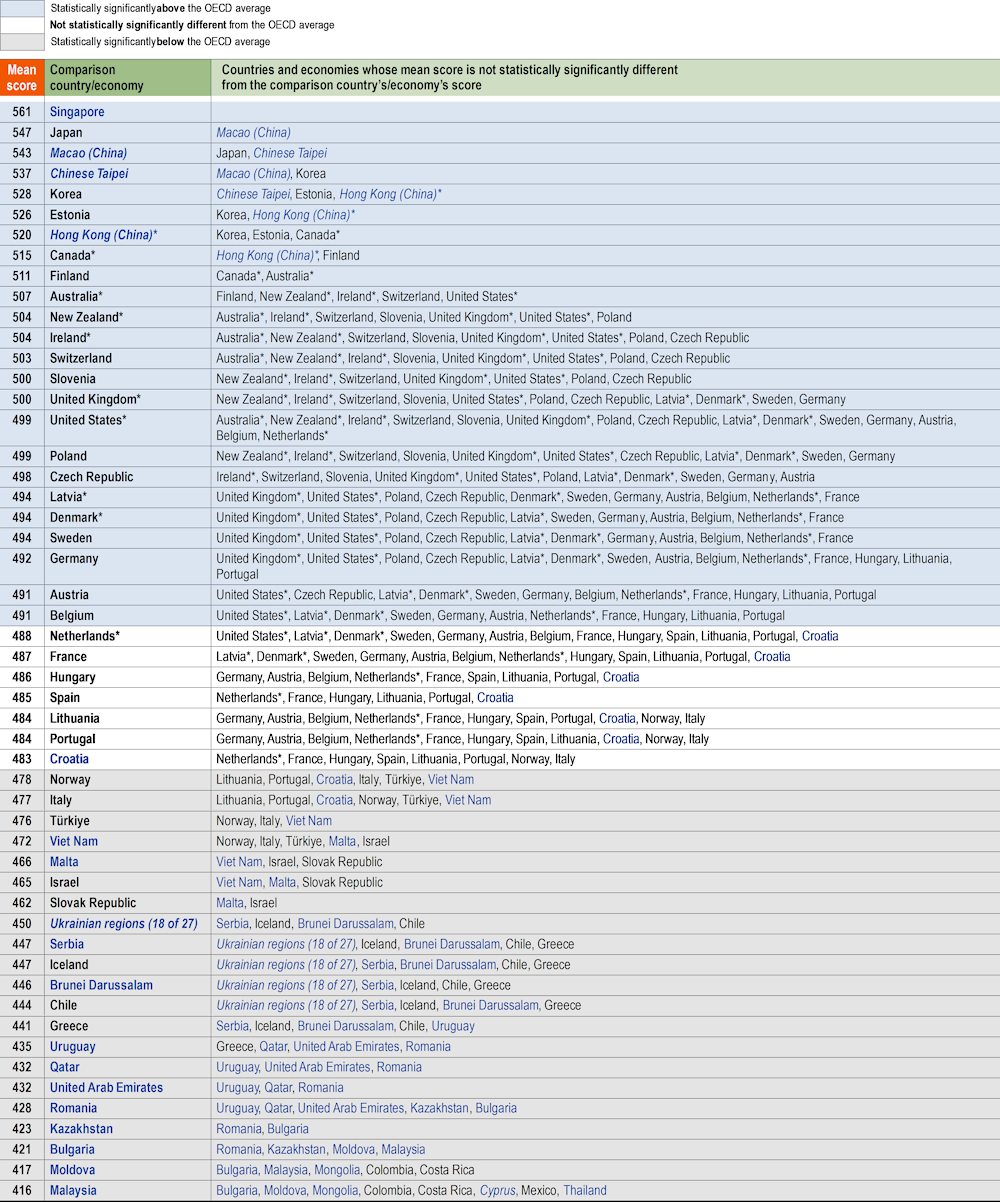
Countries and economies are ranked in descending order of the mean performance in science.
Source: OECD, PISA 2022 Database, Table I.B1.2.3.
Table I.2.3. Comparing countries’ and economies’ performance in science [2/2]
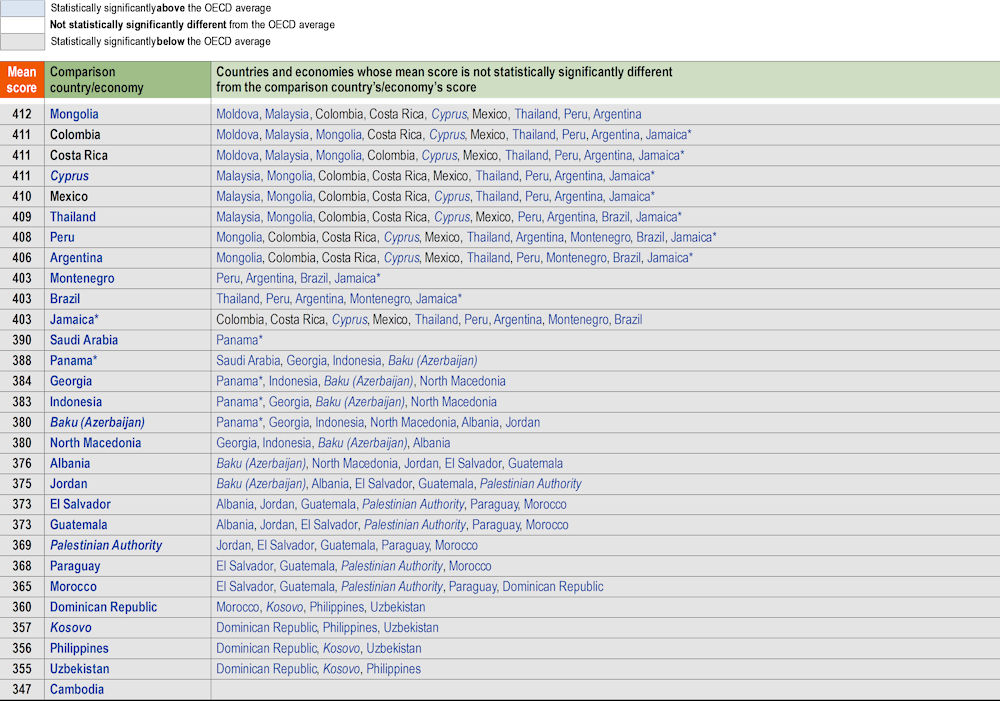
Countries and economies are ranked in descending order of the mean performance in science.
Source: OECD, PISA 2022 Database, Table I.B1.2.3.
Box I.2.1. How is student mathematics anxiety related to their performance in mathematics?
Students who perform better in mathematics have, on average, lower levels of anxiety about mathematics. In PISA, this finding was first reported in 2012 (OECD, 2013[1]) and it is also found in PISA 2022.
As examined in this box, a negative association between mathematics performance and mathematics anxiety is found in every education system that took part in PISA 2022, without exceptions. At the system level, the cross-national association between average levels of mathematics anxiety and mean mathematics performance is also negative but more variation in anxiety levels exists among top-performing countries.
Furthermore, research suggests that positive attitudes towards mathematics and learning can help students reduce their levels of mathematics anxiety and its negative consequences on mathematics performance (Choe et al., 2019[2]; Dowker, Sarkar and Looi, 2016[3]; Carey et al., 2016[4]; Goetz et al., 2010[5]; Ashcraft and Kirk, 2001[6]). As shown in the second part of this box, a growth mindset – the belief that one’s abilities and intelligence can be developed over time rather than being an invariant innate gift – is one of the positive attitudes towards learning that can alleviate mathematics anxiety.
Mathematics anxiety in PISA 2022
To measure students’ anxiety about mathematics, PISA 2022 asked students whether they agreed (“strongly disagree”, “disagree”, “agree”, or “strongly agree”) with the following six statements: “I often worry that it will be difficult for me in mathematics classes”; “I worry that I will get poor marks in mathematics”; “I get very tense when I have to do mathematics homework”; “I get very nervous doing mathematics problems”; “I feel helpless when doing a mathematics problem”; and “I feel anxious about failing in mathematics”. Data from these items was combined to create the PISA index of mathematics anxiety (ANXMAT).
Within countries/economies, mathematics anxiety is negatively associated with student achievement in mathematics in every education system that took part in PISA 2022 regardless of student and school characteristics. On average across OECD countries, a one-point increase in the index of mathematics anxiety is associated with a decrease in mathematics achievement of 18 score points after accounting for students’ and schools’ socio-economic profile (Table I.B1.2.17).
Countries/economies with higher average levels of mathematics anxiety perform less well in mathematics. International differences in the index of mathematics anxiety account for about 25% of the variation in student performance in mathematics across all countries and economies that took part in PISA 2022 (Figure I.2.1).
Figure I.2.1. Mathematics anxiety and mean score in mathematics in PISA 2022
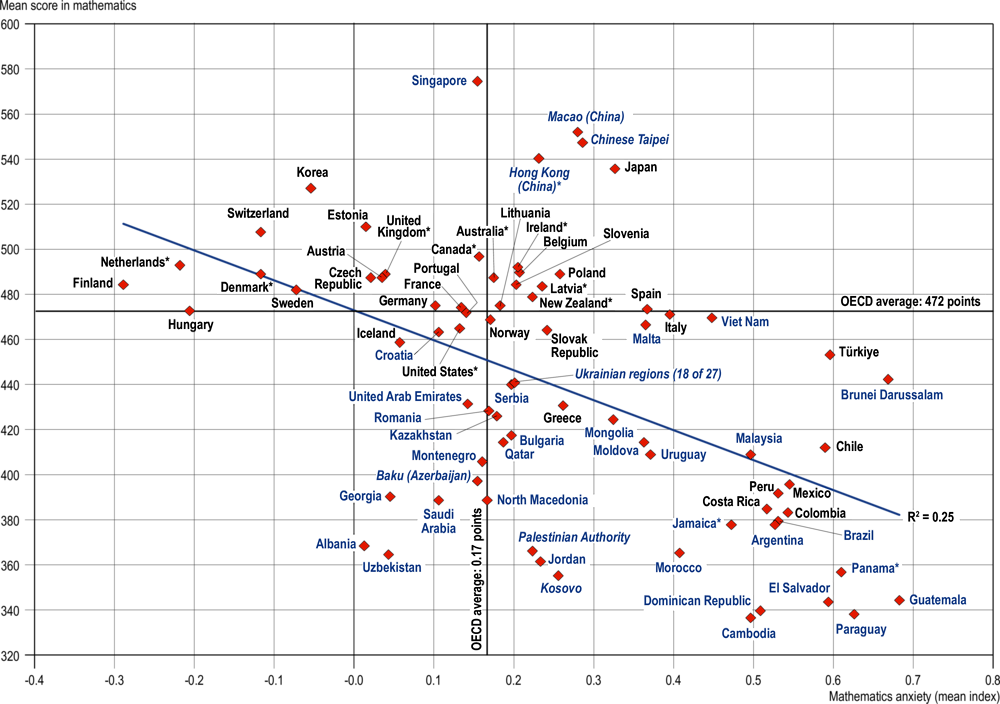
Note: Only countries and economies with available data are shown.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1 and I.B1.2.16.
Mathematics anxiety is particularly high among countries/economies with low levels of performance in mathematics. The 17 countries/economies with the highest levels of mathematics anxiety in PISA 2022 (i.e. values higher than .47 in ANXMAT) performed below the OECD average in mathematics; out of those 17 countries/economies, 13 have a mean performance in mathematics below 400 points.
Conversely, the lowest levels of anxiety tend to be in countries whose mean score in mathematics is above the OECD average, most noticeably Denmark*, Finland, the Netherlands* and Switzerland (Figure I.2.1). Nevertheless, countries/economies with high levels of performance in mathematics differ widely in their levels of mathematics anxiety. Importantly, four out of the six East Asian countries/economies that outperformed all other countries/economies in mathematics in PISA 2022 show high levels of mathematics anxiety (Hong Kong [China]*, Japan, Macao [China] and Chinese Taipei); the exceptions are Korea and Singapore, where students show levels of mathematics anxiety similar to or lower than the OECD average.
Research has addressed anxiety as a multidimensional or multifaceted construct: sources of anxiety may be as diverse as its consequences (Zeidner et al., 2005[7]). Anxiety could have at least cognitive and somatic components, and could be further disentangled from test anxiety and other types of anxiety that may have a direct impact on student performance (Zeidner et al., 2005[7]). Treating anxiety as multidimensional may help to understand why, in some countries/economies, personal and situational aspects may affect anxiety differently (Putwain, Woods and Symes, 2010[8]), and more specifically, the relationship between anxiety and performance as measured by PISA. Further research is needed on how these individual factors and other cultural dimensions (Ho et al., 2000[9]; Zhang, Zhao and Kong, 2019[10]) interact and may differentially affect students' mathematics performance in PISA.
Growth mindset and mathematics anxiety
Growth mindset can help students overcome performance-related anxiety (Yeager and Walton, 2011[11]) potentially reducing its negative consequences on performance and, ultimately, well-being (OECD, 2021[12]; Yeager et al., 2019[13]). A growth mindset, as opposed to a fixed mindset, is the belief in the malleability of ability and intelligence, and is one possible explanation why some people fulfil their potential while others do not (Dweck, 2006[14]). People with a growth mindset are more likely to work to develop their skills and be motivated when experiencing drawbacks; by contrast, individuals with fixed mindsets (who believe that people are born with certain invariant characteristics that cannot be changed) tend to favour validation of their abilities, avoid challenges and stay within their comfort zone. One characteristic of students with a growth mindset is reduced anxiety about learning, which is linked to their positive view of failure and obstacles (Dweck and Yeager, 2019[15]).
PISA 2022 asked students whether they agreed (“strongly disagree”, “disagree”, “agree”, or “strongly agree”) with the following statement: “Your intelligence is something about you that you can’t change very much”. Students strongly disagreeing or disagreeing with the statement are considered to have a growth mindset.
PISA results show that students who reported having a growth mindset have less mathematics anxiety than students with a fixed mindset on average across OECD countries (difference of -0.13 points in the mathematics anxiety index) and in 42 out of 73 countries and economies with available data (Table I.BI.2.16). Furthermore, a growth mindset is positively associated with student performance in mathematics. Students who reported having a growth mindset score better in mathematics than students with a fixed mindset even after accounting for student and school socio- economic profile on average across OECD countries (difference of 18 score points) and in 57 countries and economies (Table I.BI.2.17).
Mathematics anxiety and growth mindset are considered together in Figure I.2.2, which shows the OECD average score in mathematics for four groups of students: those with (i) high mathematics anxiety and growth mindset, (ii) high mathematics anxiety and fixed mindset, (iii) low mathematics anxiety and growth mindset, and (iv) low mathematics anxiety and fixed mindset. Students who were more anxious about mathematics scored better in mathematics if they had a growth mindset (461 score points) than if they had a fixed mindset (443 score points). Similarly, students who were less anxious about mathematics scored better if they had a growth mindset (523 score points) than if they had a fixed mindset (500 score points).
This OECD pattern is also observed in most countries with available data. In 54 out of 73 countries/economies, students with low anxiety performed better in math if they had a growth mindset rather than fixed mindset. Also, in 46 out of 73 countries/economies, students with high anxiety performed better in math if they had a growth mindset rather than fixed (Table I.BI.2.17).
This association holds even after accounting for student and school socio- economic profile (Table I.BI.2.17).
Figure I.2.2. Mathematics performance and anxiety in mathematics among students with fixed and growth mindsets
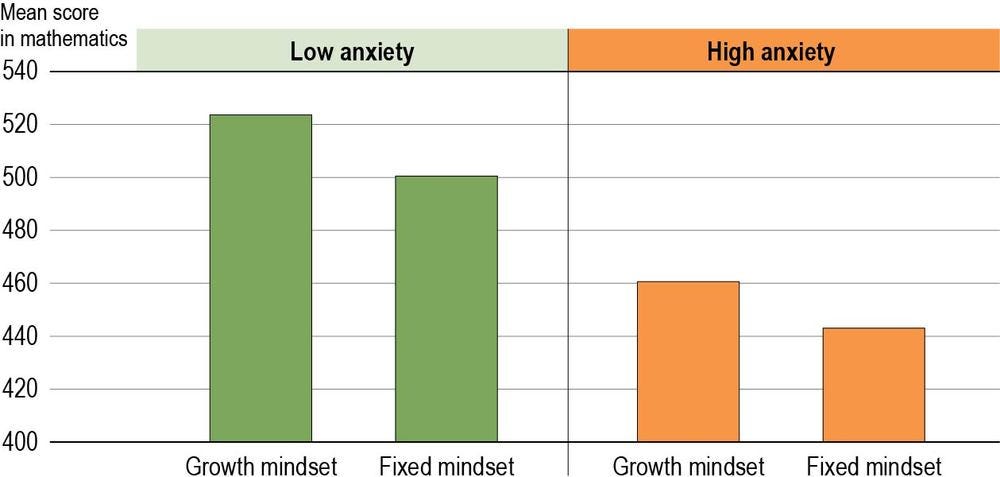
Note: Low/high anxiety are students in the bottom/top quarter of the distribution in the ANXMAT index in their own countries/economies.
Source: OECD, PISA 2022 Database, Table I.B1.2.17.
Policy implications
Mathematics anxiety can be diminished by means of mathematics training but also by improving positive attitudes towards mathematics and learning, including role models, further support in schools and fostering growth mindsets (Beilock et al., 2010[16]). To develop students’ ability to tackle real-world problems and apply mathematical knowledge successfully, schools and education systems need to go beyond formal mathematics education. To deal head-on with important barriers to mathematics learning, it is important to understand and address students’ attitudes and emotions about mathematics, and to develop positive students’ mindsets and disposition towards learning challenges and effort.
Variation in performance within and between countries and economies
Variation in performance within countries
The Dominican Republic has the smallest variation in mathematics proficiency (54 score points) while several other countries and economies whose mean performance was below the OECD average also have small variations in performance2. Variation in student performance tends to be greater among high-performing than low-performing education systems. As shown in Figure I.2.3, there is a strong correlation between average performance in mathematics and variation in performance in mathematics. That said, this is not the case for all countries. For instance, Latvia* has a mean of 483 and a standard deviation of 80.
However, among countries that performed above the OECD average, Ireland*, Latvia* and Denmark* stand out for their relatively small variation in performance (standard deviation around 80 score points) (Figure I.2.3). Similarly, among countries that performed below the OECD average, Bulgaria, Israel, Malta, Romania, the Slovak Republic and the United Arab Emirates, stand out for their relatively large variation in performance (standard deviation greater than 95 score points).
Figure I.2.3. Average performance in mathematics and variation in performance
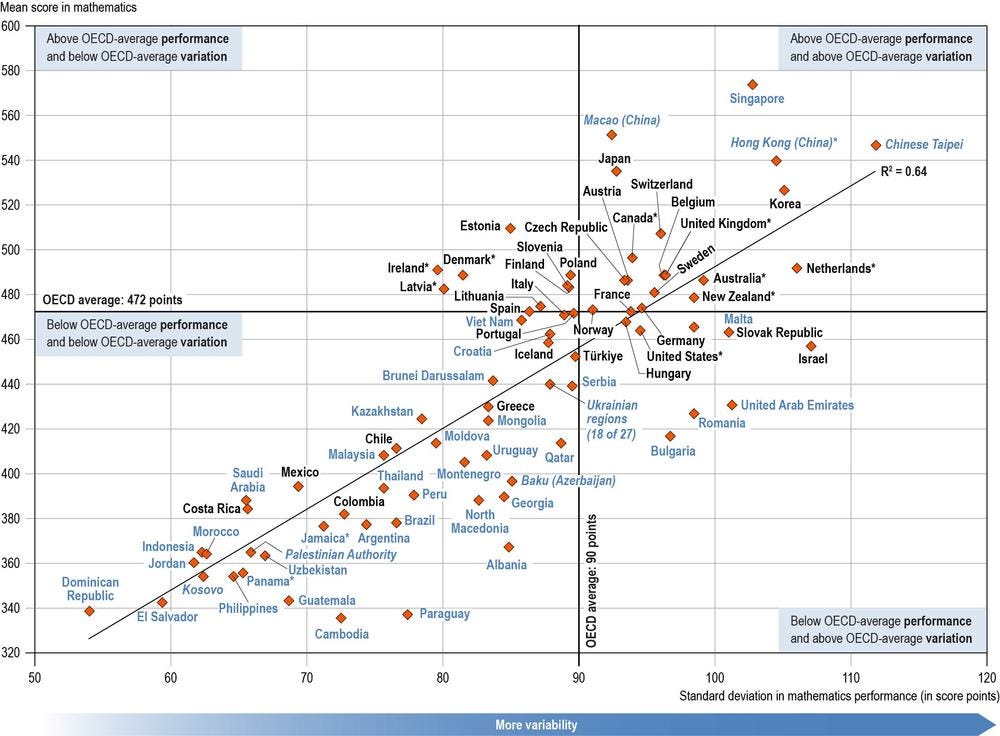
Source: OECD, PISA 2022 Database, Table I.B1.2.1.
Another measure of variation in performance within countries is the score gap that separates the highest- and lowest-performing students within a country (i.e. inter-decile range). In mathematics, the difference between the 90th percentile of performance (the score above which only 10% of students scored) and the 10th percentile of performance (the score below which only 10% of students scored) is more than 135 score points in all countries and economies; on average across OECD countries, 235 score points separate these extremes (Figure I.2.4).
The largest differences between top-performing and low-achieving students in mathematics are found in Israel, the Netherlands* and Chinese Taipei (Figure I.2.4). In these countries, the inter-decile range is 280 score points or more, which means that student performance in mathematics is highly unequal across 15-year-olds.
By contrast, the smallest differences between high- and low-achieving students are found among countries and economies with low (i.e. lower than 370 points) mean scores (the Dominican Republic, El Salvador, Indonesia, Jordan and Kosovo). In these countries, the 90th percentile of the mathematics distribution is below the average score across OECD countries.
Figure I.2.4. Mean score in mathematics at 10th, 50th and 90th percentile of performance distribution
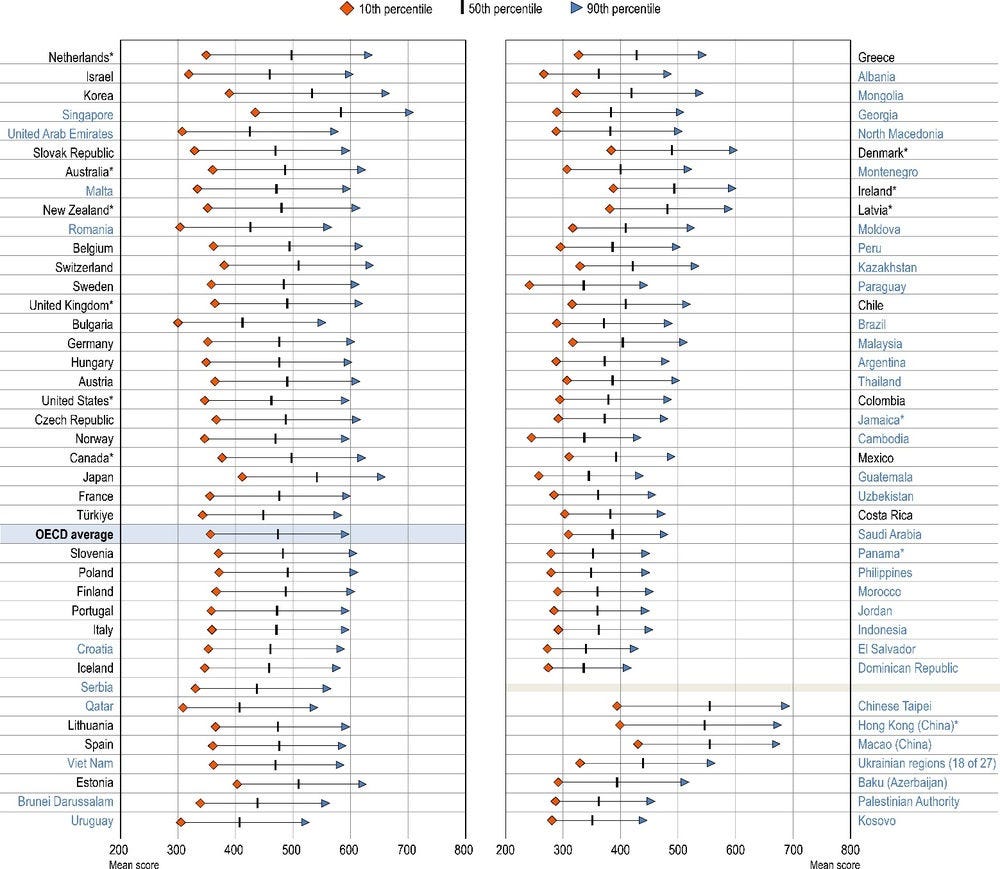
Note: All differences between the 90th and the 10th percentiles are statistically significant (see Annex A3).
Countries and economies are ranked in descending order of the difference in mathematics performance between 90th percentile and 10th percentile.
Source: OECD, PISA 2022 Database, Table I.B1.2.1.
Performance differences among educational systems, schools and students
Student performance varies widely among 15-year-olds and that variation can be broken down into differences at the student, school and education system levels3. This analysis is important from a policy perspective. Pinpointing where differences in student performance lie enables education stakeholders to target policy4. For example, if a large percentage of the total variation in student performance is linked to differences in student performance between education systems, this means that education system characteristics (e.g. economic and social conditions, education policies) strongly influence student performance. Similarly, if differences between schools account for a significant part of the overall variation in performance within a country/economy, then differences in school characteristics are important for policy to consider.
In PISA 2022, about 31% of the variation in mathematics performance is linked to mean differences in student performance between participating education systems (Figure I.2.5) across all countries and economies. This means that the characteristics of education systems have a great deal of influence on student performance. As shown in Chapter 4, the economic and social conditions of different countries/economies, which are often beyond the control of education policy makers and educators, can influence student performance by means of, for example, wealthier countries spending more on education than mid- and low-income countries. On the other hand, it is education policy makers and educators who determine education policies and practices, including the organisation of schooling and learning, and the allocation of available resources across schools and students.
Across OECD countries, however, only 12% of the variation in mathematics performance is between education systems. In other words, the characteristics of education systems do not play an important role in explaining differences in student performance among OECD countries. This is likely because the economic and social conditions of OECD countries are very similar to each other. It is also possible that education policies and practices vary less across OECD countries than across all PISA-participating countries.
Figure I.2.5. Variation in mathematics performance between systems, schools and students
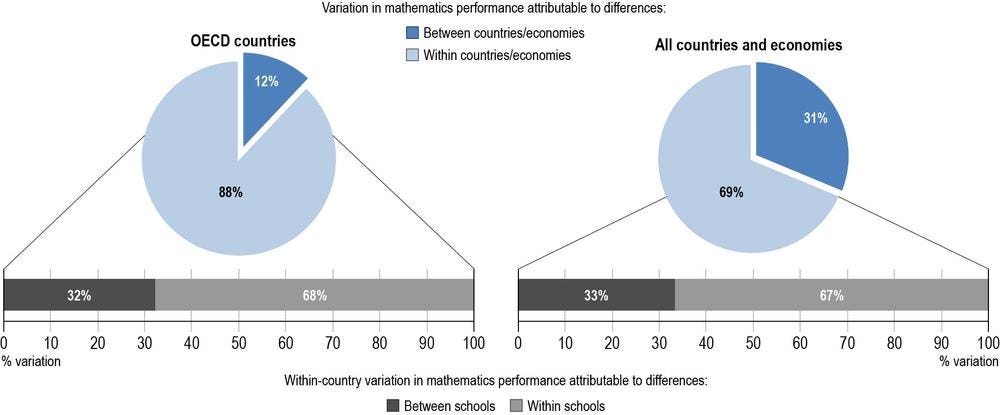
Source: OECD, PISA 2022 Database.
Out of the variation observed within countries in PISA 2022, 32% of the OECD average variation in mathematics performance is between schools (right side of Figure I.2.6); the remaining part of the variation (68%) is within schools (left side of the figure). This means that school characteristics do not play a dominant role in explaining student performance; instead, it is the characteristics of students themselves (i.e. their background, attitudes and behaviour, etc.), and the characteristics of different classrooms and different grades within schools that account for most of the overall variation in student performance.
The extent of between-school variation in mathematics performance differs widely across countries/economies. In six countries and economies between-school differences account for 10% or less of the total variation in performance (Iceland, Saudi Arabia, Ireland*, Finland, Denmark* and Uzbekistan, in ascending order). By contrast, in 10 other countries (Bulgaria, Hungary, Israel, Japan, the Netherlands*, Romania, the Slovak Republic, Chinese Taipei, Türkiye and the United Arab Emirates) differences between schools account for at least 50% of the total variation in the country’s performance.
Figure I.2.6. Variation in mathematics performance between and within schools
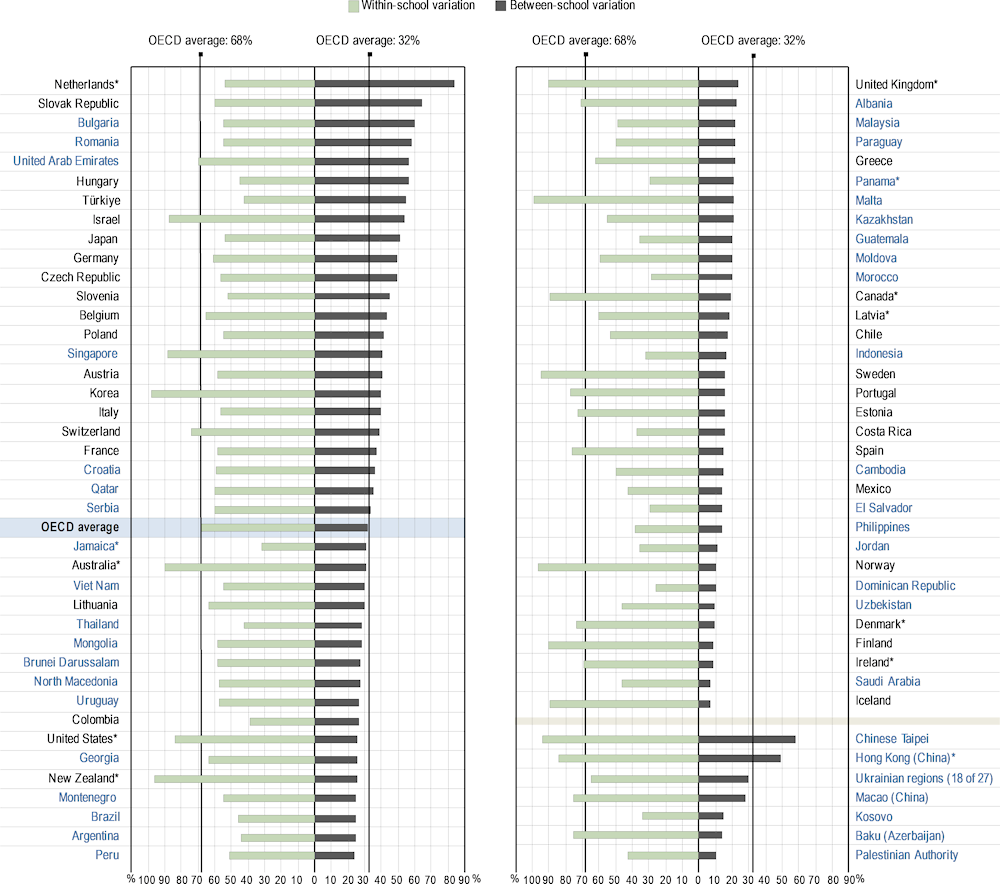
Note: This figure is restricted to schools with the modal ISCED level for 15-year-old students5.
Countries and economies are ranked in descending order of the between-school variation in mathematics performance as a percentage of the total variation in performance across OECD countries.
Source: OECD, PISA 2022 Database, Table I.B1.2.12.
Ranking countries’ and economies’ performance in PISA
The goal of PISA is to provide useful information to educators and policy makers on the strengths and weaknesses of their country’s education system, their progress made over time, and opportunities for improvement. When ranking countries’ and economies’ student performance in PISA, it is important to consider the social and economic context of schooling (see next section). Moreover, many countries and economies score at similar levels; small differences that are not statistically significant or practically meaningful should not be considered (see Box 1 in Reader’s Guide).
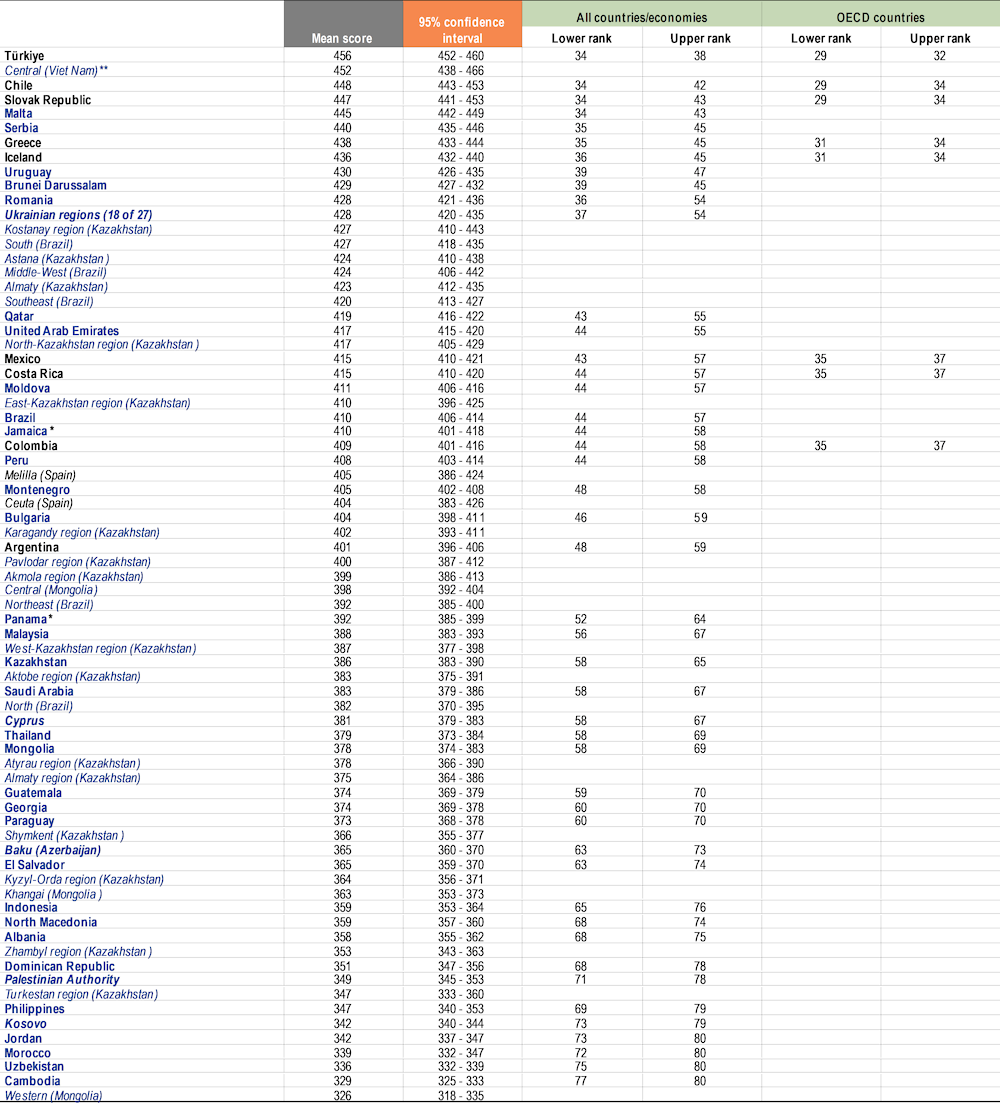
Table I.2.4, Table I.2.5 and Table I.2.6 show for each country and economy an estimate of where its mean performance ranks among all other countries and economies that participated in PISA as well as, for OECD countries, among all OECD countries. Because mean-score estimates are derived from samples and are thus associated with statistical uncertainty, it is often not possible to determine an exact ranking for all countries and economies. However, it is possible to identify the range of possible rankings for the country’s or economy’s mean performance6. This range of ranks can be wide, particularly for countries/economies whose mean scores are similar to those of many other countries/economies.
Table I.2.4, Table I.2.5 and Table I.2.6 also include the results of provinces, regions, states or other subnational entities within the country for countries where the sampling design supports such reporting. For these subnational entities, a rank order was not estimated. Still, the mean score and its confidence interval allow the performances of subnational entities and countries/economies to be compared. For example, Quebec (Canada*) scored below top-performers Macao (China), Singapore, Chinese Taipei and Hong Kong (China)*, but close to Korea in mathematics.
Table I.2.4. Mathematics performance at national and subnational levels [1/2]
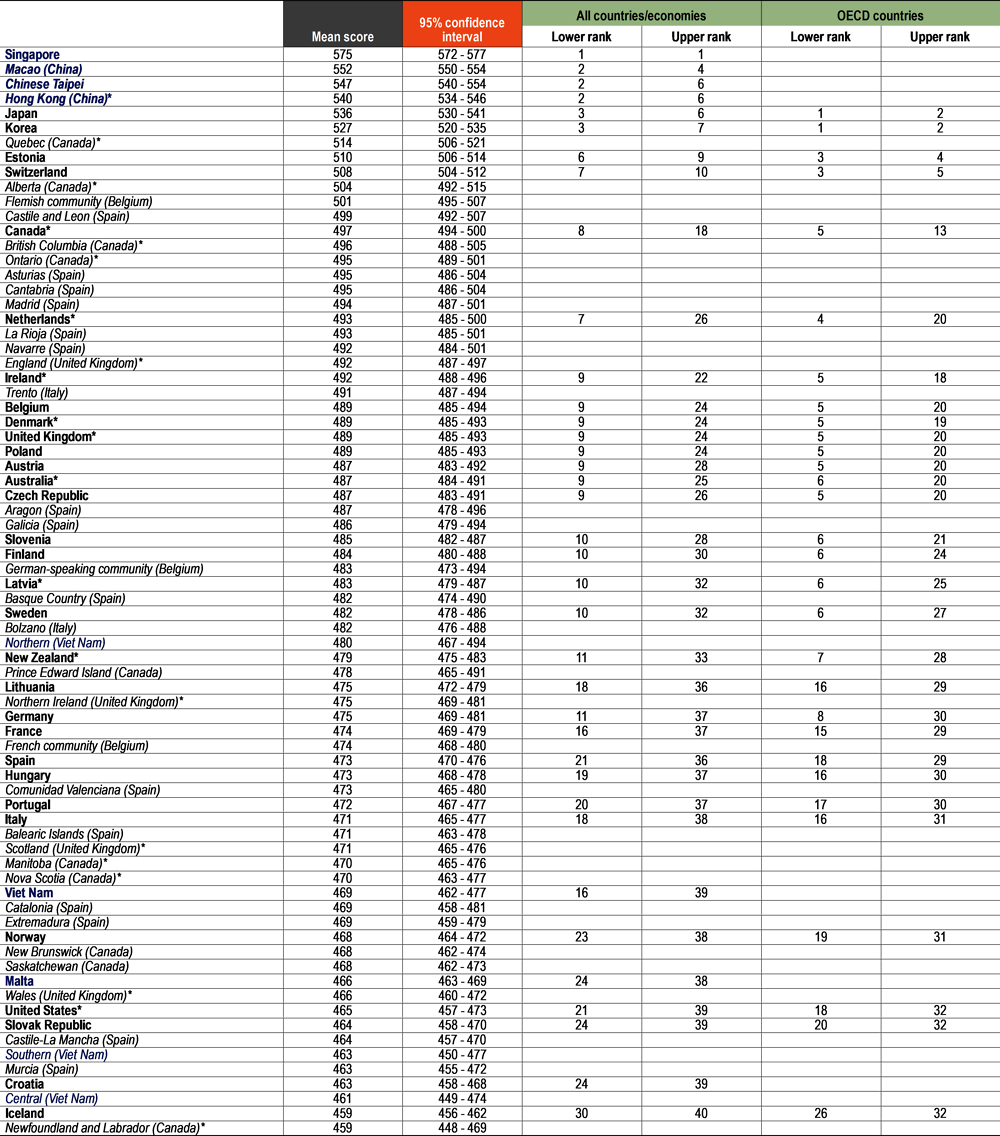
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in mathematics.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1 and I.B2.2.1.
Table I.2.4. Mathematics performance at national and subnational levels [2/2]
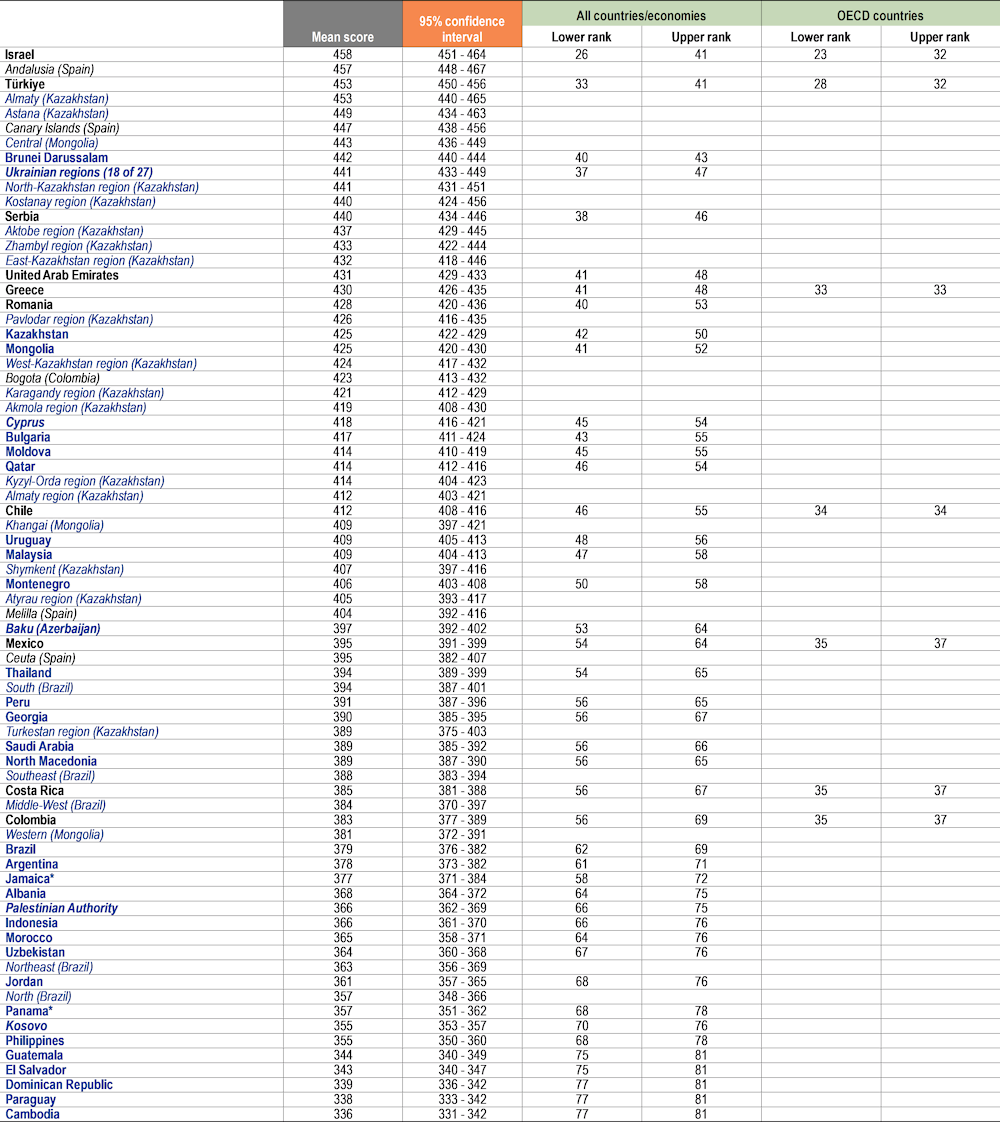
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in mathematics.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1 and I.B2.2.1.
Table I.2.5. Reading performance at national and subnational levels [1/2]
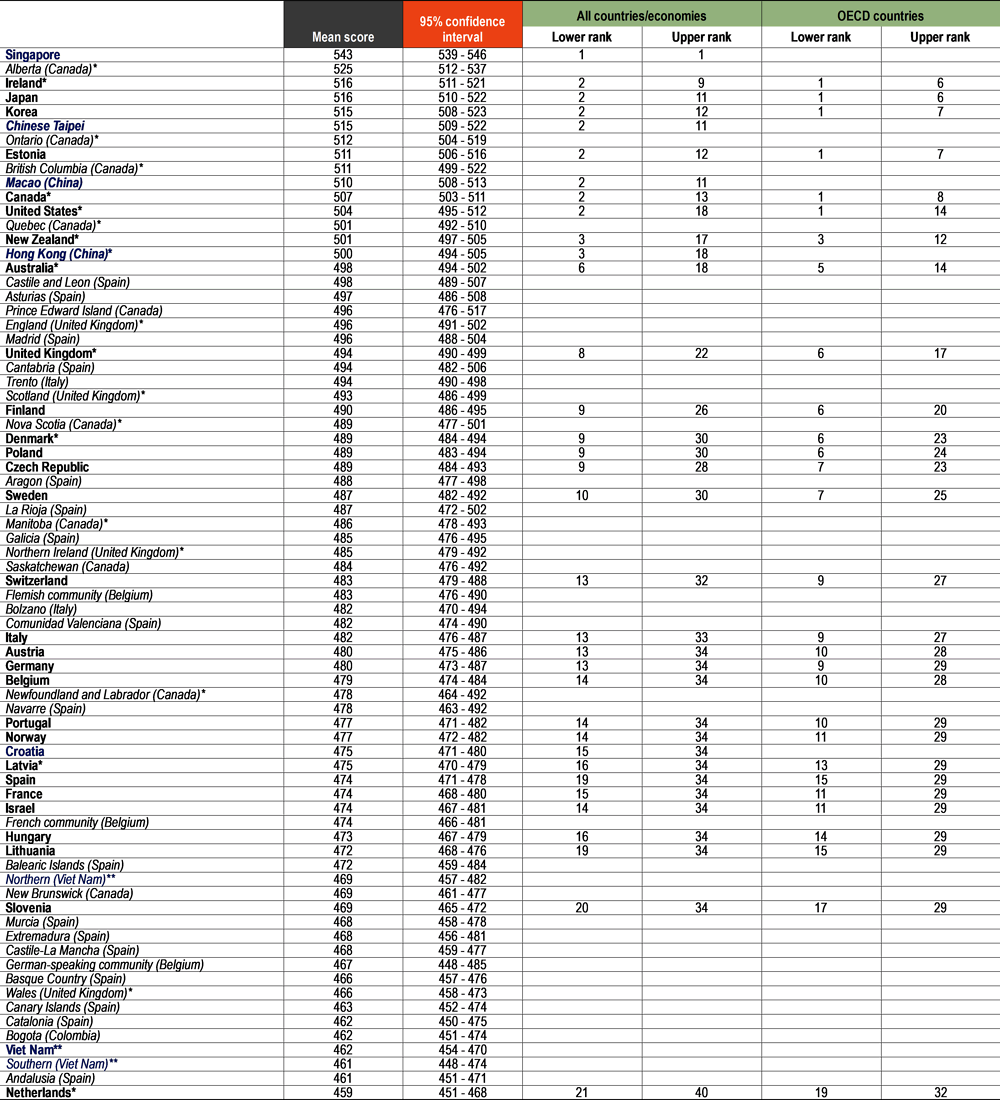
** Caution is required when comparing estimates based on PISA 2022 with other countries/economies as a strong linkage to the international PISA reading scale could not be established (see Reader's Guide and Annex A4).
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in reading.
Source: OECD, PISA 2022 Database, Table I.B1.2.2 and Table I.B2.2.
Table I.2.5. Reading performance at national and subnational levels [2/2]
** Caution is required when comparing estimates based on PISA 2022 with other countries/economies as a strong linkage to the international PISA reading scale could not be established (see Reader's Guide and Annex A4).
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in reading.
Source: OECD, PISA 2022 Database, Table I.B1.2.2 and Table I.B2.2.
Table I.2.6. Science performance at national and subnational levels [1/2]
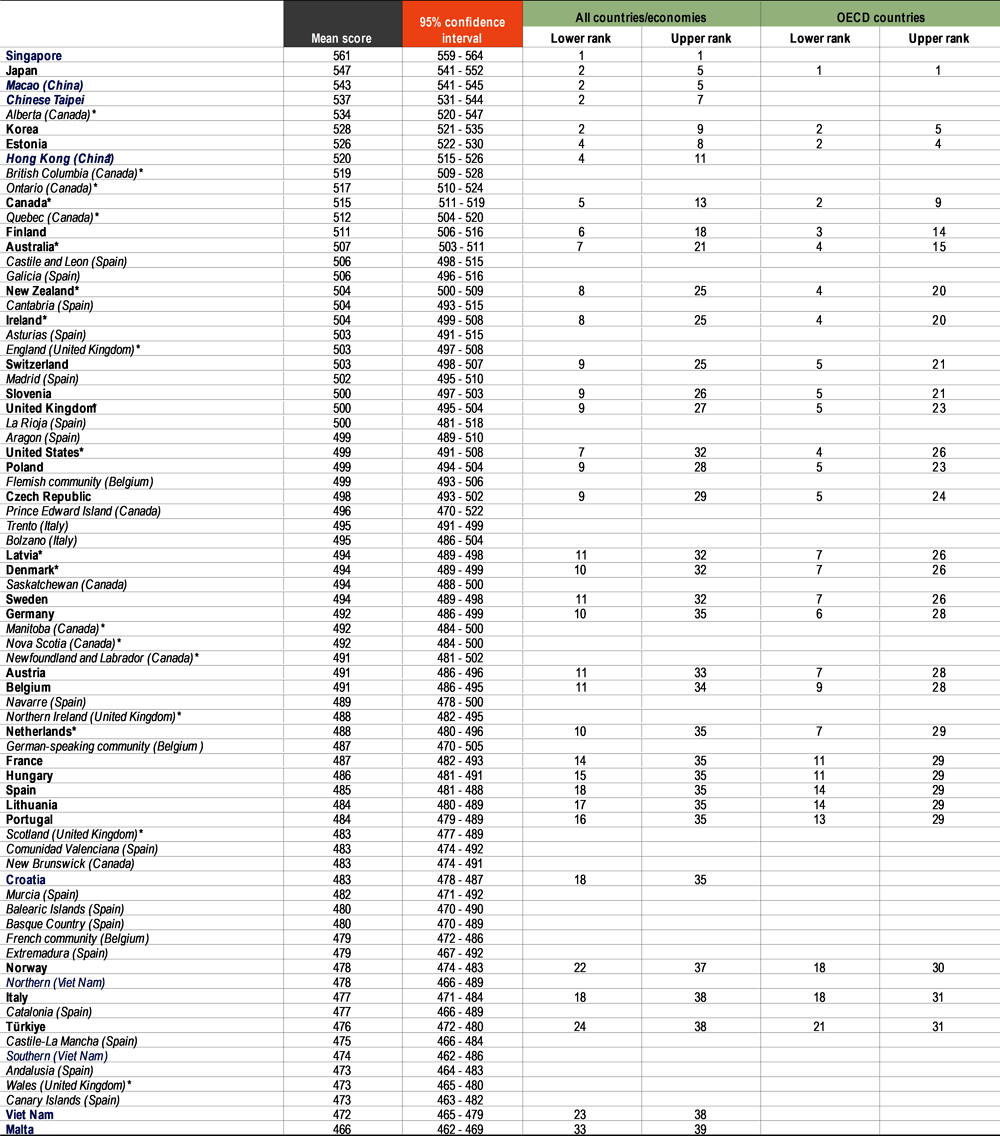
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in science.
Source: OECD, PISA 2022 Database, Table I.B1.2.3 and Table I.B2.3.
Table I.2.6. Science performance at national and subnational levels [2/2]
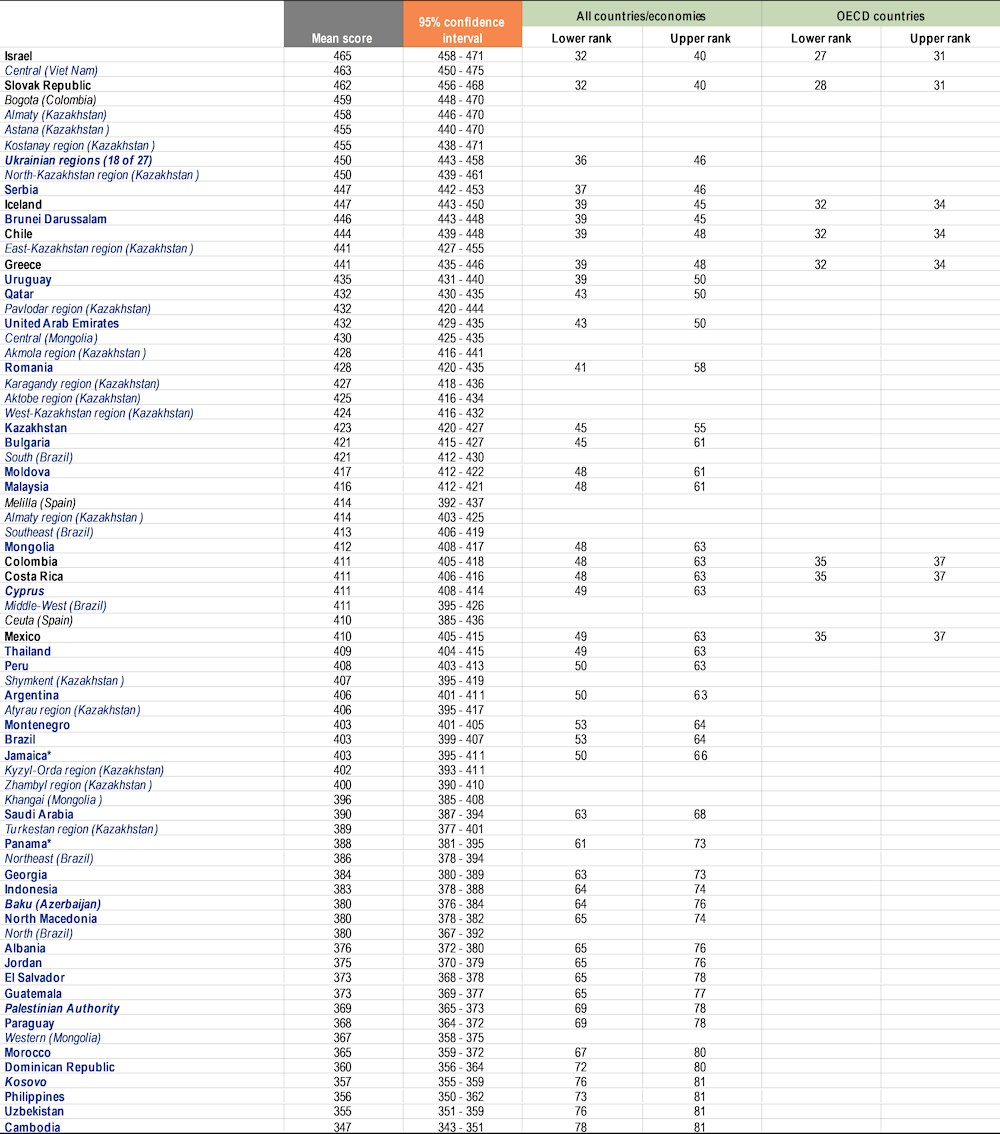
Notes: OECD countries are shown in bold black. Partner countries and economies are shown in bold blue. Provinces, regions, states or other subnational entities are shown in black italics (OECD countries) or blue italics (partner countries).
Range-of-rank estimates are computed based on mean and standard-error-of-the-mean estimates for each country/economy, and take into account multiple comparisons amongst countries and economies at similar levels of performance. For an explanation of the method, see Annex A3. For subnational entities, a rank order was not estimated.
Countries and economies are ranked in descending order of the mean performance in science.
Source: OECD, PISA 2022 Database, Table I.B1.2.3 and Table I.B2.3.
Average performance in different aspects of mathematics competence
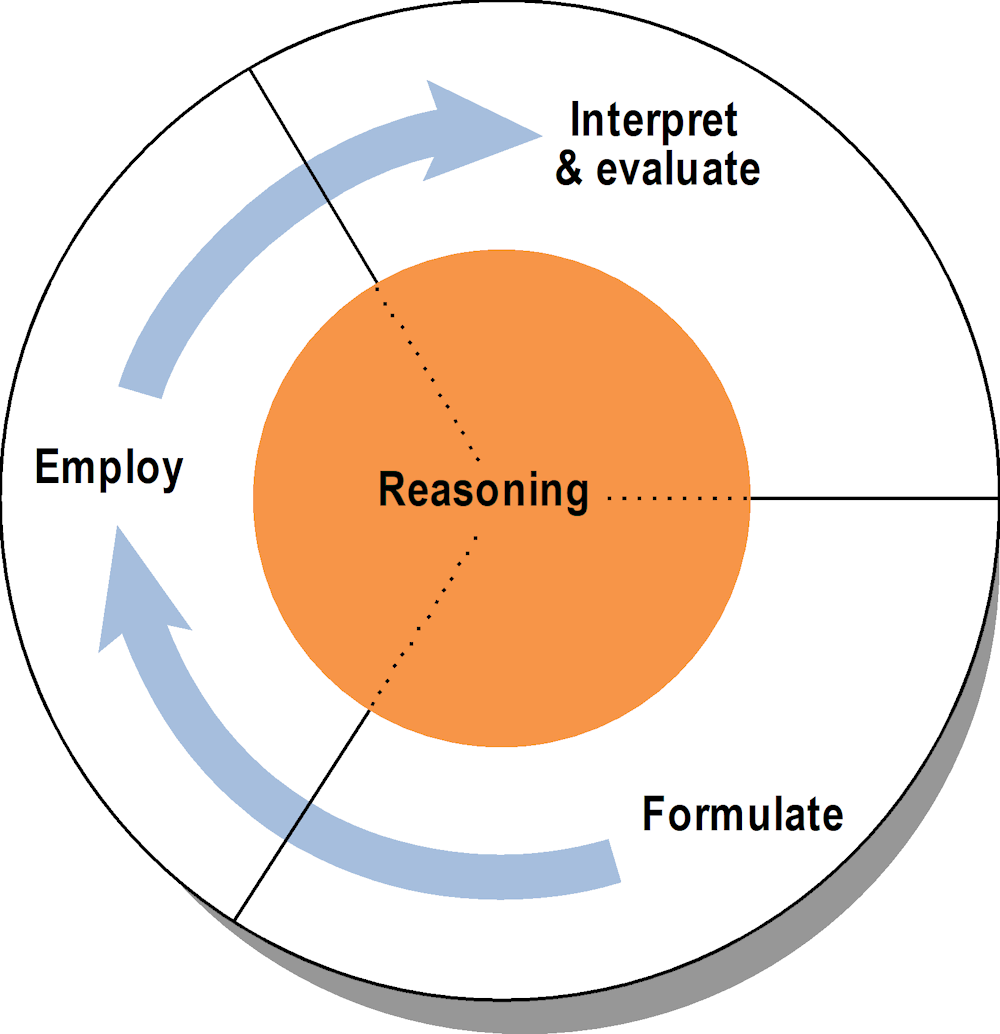
This section focuses on student performance in two sets of mathematics subscales: process subscales and content subscales. Each item in the PISA 2022 computer-based mathematics assessment was classified into one of the four mathematics-processes subscales of formulating, employing, interpreting, and reasoning. Similarly, each item in the PISA 2022 computer-based mathematics assessment was classified into one of the four mathematics-content subscales of change and relationships, space and shape, quantity, and uncertainty and data.
The relative strengths and weaknesses of each country’s/economy’s education system are analysed by looking at differences in mean performance across the PISA mathematics subscales within the process and content subscales. See Annex A1 for detailed definitions of subscales.
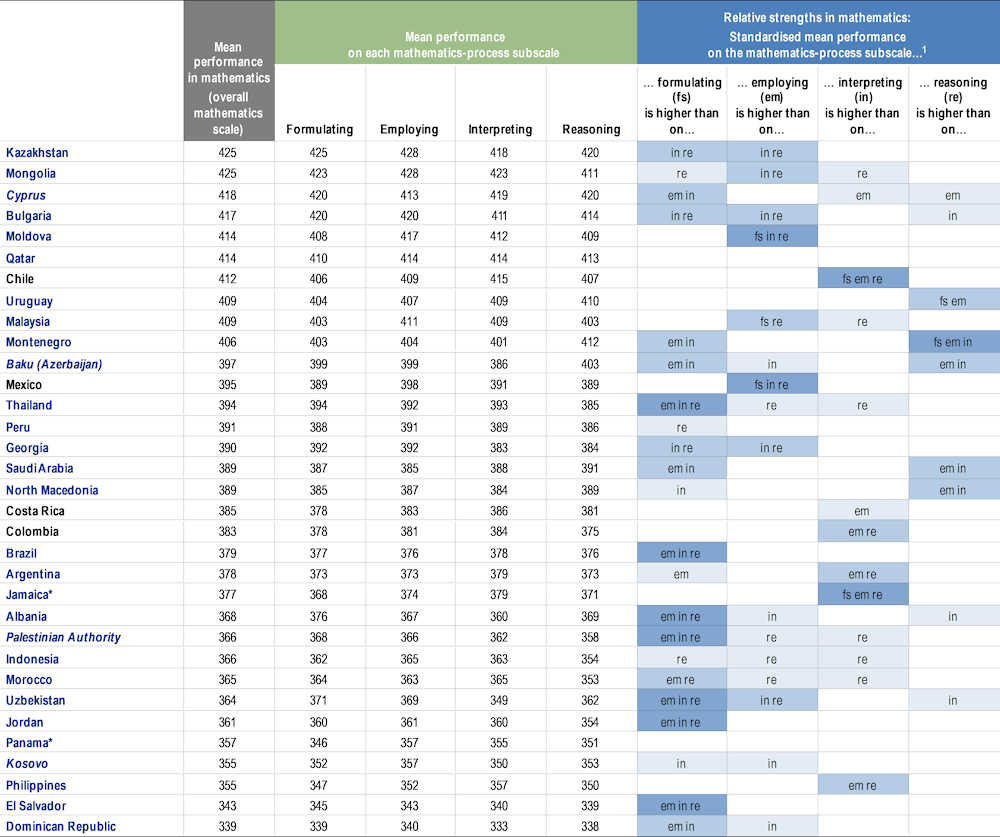
Table I.2.7 shows the country/economy mean for the overall mathematics scale and for each of the four mathematics-process subscales. It also points to which differences along the (standardised) subscale means are significant, indicating a country’s/economy’s relative strengths and weaknesses.
For example, in Japan mean performance in mathematics is 536 score points. Japan’s score is also 536 points in the mathematics-processes subscales of formulating and employing, and the score is very similar (534 points) in the process subscale of reasoning. However, in the interpreting process, the score is considerably higher (544 points). Compared to differences in how students performed in different subscales on average across PISA-participating countries/economies (i.e. hereafter, for simplicity, the “worldwide average”), students in Japan are stronger at interpreting than all other mathematics-process subscales.
On average across OECD countries, students are relatively stronger at interpreting than formulating and stronger at interpreting than employing, compared to the worldwide average. In addition, students are relatively stronger at reasoning than formulating and employing, and relatively stronger at employing than formulating on average across OECD countries compared to the worldwide average. The same pattern of relative strengths was observed in Spain and the United Kingdom*. In Belgium, Canada*, Korea and New Zealand*, the pattern is the same as the OECD average except that there are no significant differences in how students performed in formulating and employing.
In 22 countries/economies, students are relatively stronger at reasoning than formulating; in 23 countries/economies, students are relatively stronger at reasoning than employing; and in 17 countries/economies, students are relatively stronger at reasoning than interpreting, compared to the worldwide average.
In six countries/economies, there are no significant differences in how students performed across different mathematics-process subscales. For example, in Latvia*, overall mean performance in mathematics is 483 score points with 483 points in formulating; 484 points in employing; 485 points in interpreting; and 481 points in reasoning. The same homogeneity in performance across mathematics-process subscales is observed in Malta, Panama*, Qatar, Serbia and Türkiye.
Table I.2.7. Comparing countries and economies on the mathematics-process subscales [1/2]
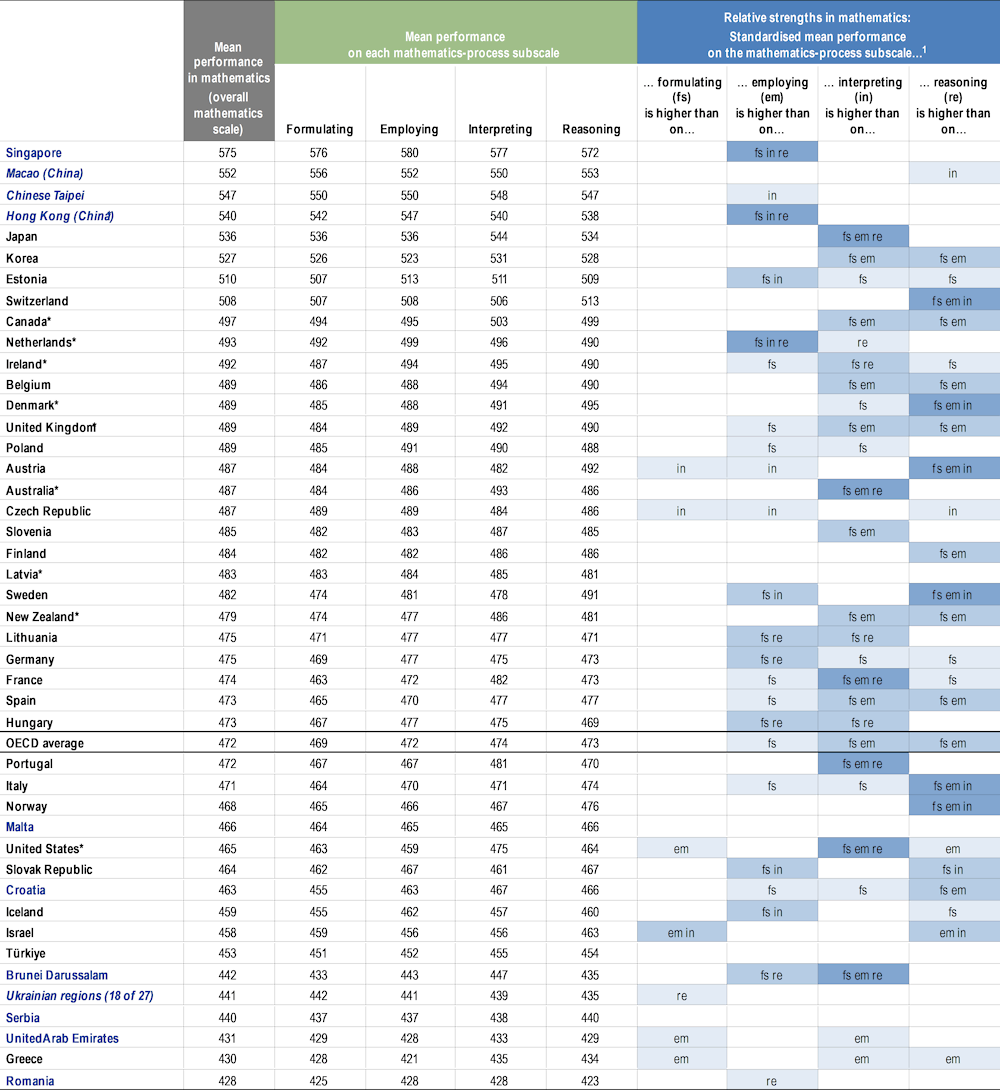
1. Relative strengths that are statistically significant are highlighted in a darker tone; empty cells indicate cases where the standardised subscale score is not significantly higher compared to other subscales, including cases in which it is lower. A country/economy is relatively stronger in one subscale than another if its standardised score, as determined by the mean and standard deviation of student performance in that subscale across all participating countries/economies, is significantly higher in the first subscale than in the second subscale. Process subscales are indicated by the following abbreviations: fs - formulating; em - employing; in - interpreting; re - reasoning.
Notes: Only countries and economies where PISA 2022 was delivered on computer are shown.
Although the OECD mean is shown in this table, the standardisation of subscale scores was performed according to the mean and standard deviation of students across all PISA-participating countries/economies.
The standardised scores that were used to determine the relative strengths of each country/economy are not shown in this table.
Countries and economies are ranked in descending order of mean mathematics performance.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1, I.B1.2.4, I.B1.2.5, I.B1.2.6 and I.B1.2.7.
Table I.2.7. Comparing countries and economies on the mathematics-process subscales [2/2]
1. Relative strengths that are statistically significant are highlighted in a darker tone; empty cells indicate cases where the standardised subscale score is not significantly higher compared to other subscales, including cases in which it is lower. A country/economy is relatively stronger in one subscale than another if its standardised score, as determined by the mean and standard deviation of student performance in that subscale across all participating countries/economies, is significantly higher in the first subscale than in the second subscale. Process subscales are indicated by the following abbreviations: fs - formulating; em - employing; in - interpreting; re - reasoning.
Notes: Only countries and economies where PISA 2022 was delivered on computer are shown.
Although the OECD mean is shown in this table, the standardisation of subscale scores was performed according to the mean and standard deviation of students across all PISA-participating countries/economies.
The standardised scores that were used to determine the relative strengths of each country/economy are not shown in this table.
Countries and economies are ranked in descending order of mean mathematics performance.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1, I.B1.2.4, I.B1.2.5, I.B1.2.6 and I.B1.2.7.
Content subscales
Table I.2.8 shows the country/economy mean for the overall mathematics scale and for each of the four mathematics-content subscales, and an indication of relative strengths in the mathematics content subscales.
On average across OECD countries, students are relatively stronger in uncertainty and data than change and relationships, and relatively stronger in uncertainty and data than space and shape, compared to the worldwide average. In addition, students are relatively stronger in space and shape than change and relationships; and relatively stronger in quantity than change and relationships on average across OECD countries, compared to the worldwide average.
In 27 countries/economies, students are, as in the OECD average, relatively stronger in uncertainty and data than space and shape, compared to the worldwide average. In 13 countries/economies, students are relatively stronger in uncertainty and data than change and relationships, compared to the worldwide average.
By contrast, in 24 countries/economies, students are relatively stronger in space and shape than uncertainty and data. In 19 countries/economies, students are relatively stronger in change and relationships than uncertainty and data.
Table I.2.8. Comparing countries and economies on the mathematics-content subscales [1/2]
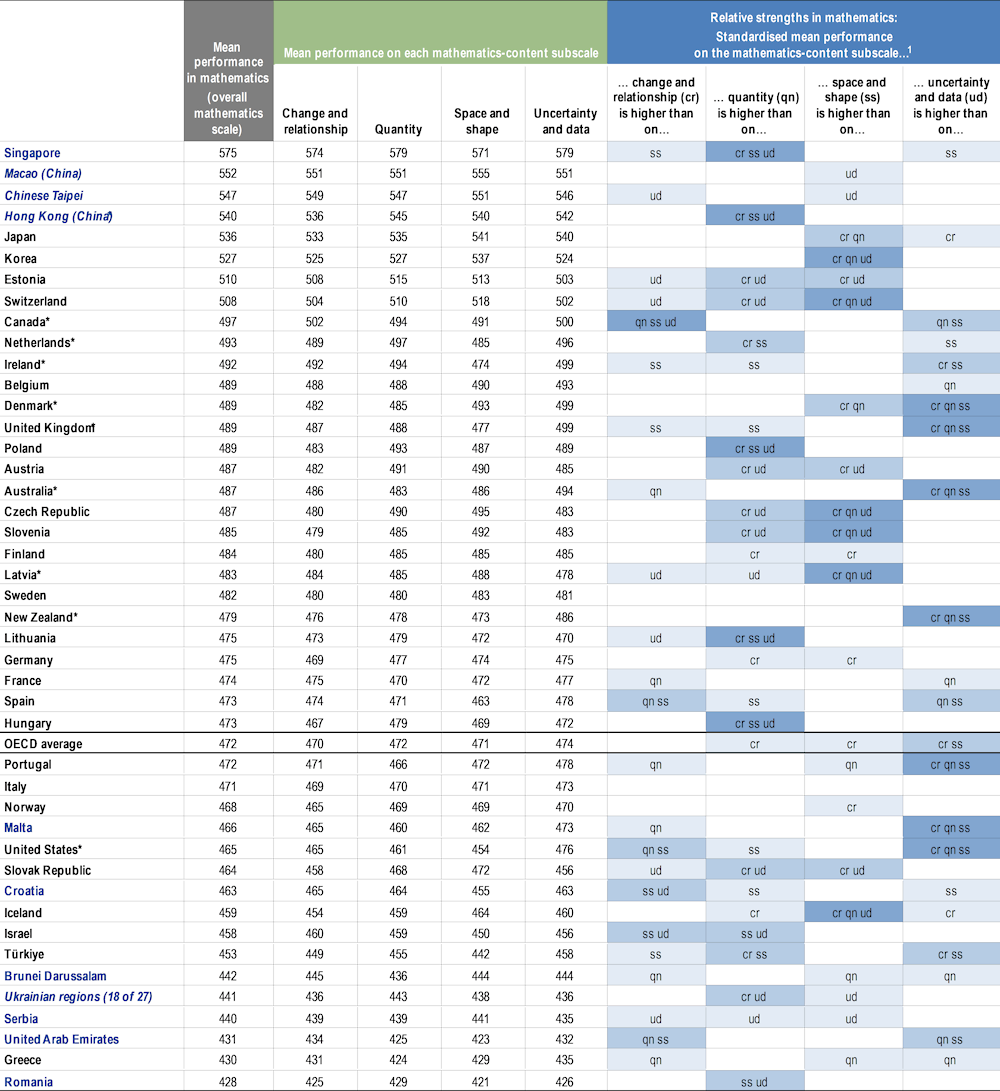
1. Relative strengths that are statistically significant are highlighted in a darker tone; empty cells indicate cases where the standardised subscale score is not significantly higher compared to other subscales, including cases in which it is lower. A country/economy is relatively stronger in one subscale than another if its standardised score, as determined by the mean and standard deviation of student performance in that subscale across all participating countries/economies, is significantly higher in the first subscale than in the second subscale. Content subscales are indicated by the following abbreviations: cr - change and relationship; qn - quantity; ss - space and shape; ud - uncertainty and data.
Notes: Only countries and economies where PISA 2022 was delivered on computer are shown.
Although the OECD mean is shown in this table, the standardisation of subscale scores was performed according to the mean and standard deviation of students across all PISA-participating countries/economies.
The standardised scores that were used to determine the relative strengths of each country/economy are not shown in this table.
Countries and economies are ranked in descending order of mean mathematics performance.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1, I.B1.2.8, I.B1.2.9, I.B1.2.10 and I.B1.2.11.
Table I.2.8. Comparing countries and economies on the mathematics-content subscales [2/2]

1. Relative strengths that are statistically significant are highlighted in a darker tone; empty cells indicate cases where the standardised subscale score is not significantly higher compared to other subscales, including cases in which it is lower. A country/economy is relatively stronger in one subscale than another if its standardised score, as determined by the mean and standard deviation of student performance in that subscale across all participating countries/economies, is significantly higher in the first subscale than in the second subscale. Content subscales are indicated by the following abbreviations: cr - change and relationship; qn - quantity; ss - space and shape; ud - uncertainty and data.
Notes: Only countries and economies where PISA 2022 was delivered on computer are shown.
Although the OECD mean is shown in this table, the standardisation of subscale scores was performed according to the mean and standard deviation of students across all PISA-participating countries/economies.
The standardised scores that were used to determine the relative strengths of each country/economy are not shown in this table.
Countries and economies are ranked in descending order of mean mathematics performance.
Source: OECD, PISA 2022 Database, Tables I.B1.2.1, I.B1.2.8, I.B1.2.9, I.B1.2.10 and I.B1.2.11.
Box I.2.2. How much do students improve in mathematics after age 15?
PISA offers a snapshot of 15-year-old students’ proficiency in mathematics, reading and science. But how does proficiency in these areas continue to evolve over students’ lives? Does it improve after they leave compulsory education? And, if it does, by how much?
The OECD Skills Outlook 2021 has published analyses combining data from PISA (2000, 2003 and 2006 assessments) and the Survey of Adult Skills, a product of the OECD Programme for the International Assessment of Adult Competencies (PIAAC) (2012 and 2015 assessment) to examine the growth in literacy and numeracy achievement between the ages of 15 and young adulthood (OECD, 2021[17]). These analyses show limited growth in achievement: across OECD countries, 15-year-olds have an average score of 268 on the PIAAC proficiency scale and in the years following compulsory schooling, their gain in literacy is on average 14 points. For numeracy, the gain in young adulthood is 28 points from a baseline PIAAC score of 269 at age 151. Analyses also explore how this achievement growth relates to students’ level of performance and their socio-economic status. In this box we present the analyses focusing on achievement growth in numeracy.
Performance growth in numeracy between age 15 and 24
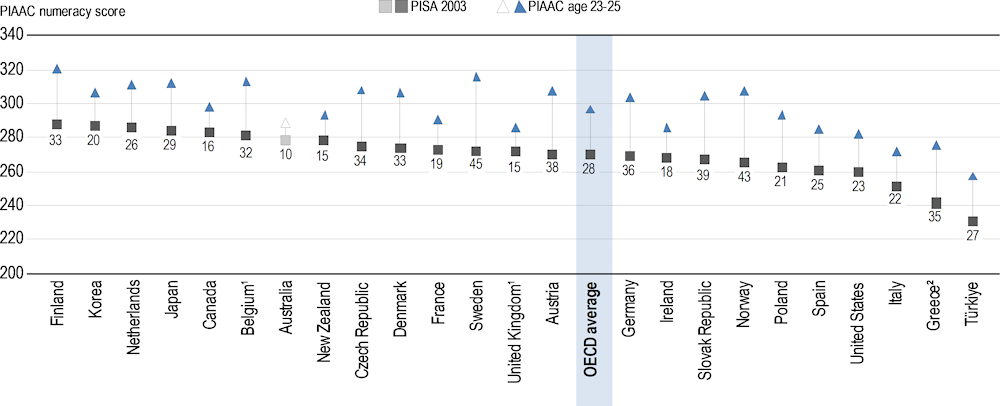
Figure I.2.7 shows the growth in numeracy performance between the ages of 15 and 24 for 24 OECD countries with available data. The blue square represents the score of 15-year-olds from the 2003 PISA test and the black triangles represent the scores of the same cohort tested in the 2012 and 2015 PIAAC surveys at around the age of 24 (for coverage and representativeness reasons, the PIAAC age range was extended to include people born one year before and after the relevant PISA cohort, in this case 24-year-olds2).
Figure I.2.7. Performance growth in numeracy between ages 15 and 24
1. In PIAAC, data for Belgium refer only to Flanders and data for the United Kingdom* refer to England and Northern Ireland jointly.
2. The data for Greece include a large number of cases (1 032) in which there are responses to the background questionnaire but where responses to the assessment are missing. Proficiency scores have been estimated for these respondents based on their responses to the background questionnaire and the population model used to estimate plausible values for responses missing by design derived from the remaining 3 893 cases.
Notes: Only OECD countries with available information are shown. Differences between age 15 and ages 23-25 that are statistically significant are shown in a darker tone (see Annex A3).
PIAAC data refers to 2012 except for Chile, Greece, Israel and New Zealand, which refer to 2015. PISA mathematics scores are expressed in PIAAC numeracy scores, following (Borgonovi et al., 2017[18]) and based on methods described in the OECD Skills Outlook 2021 (OECD, 2021[17]), Chapter 3, Box 3.1.
Countries are ranked in descending level of achievement among 15 year olds.
Source: OECD Skills Outlook 2021 (OECD, 2021[17]), Table 3.8b.
As shown in the figure, performance in numeracy increased between the ages of 15 and 24 in every country with available data, except Australia*. On average across the 24 OECD countries, performance in numeracy increased by 28 points on the PIAAC numeracy scale, from 269 to 297 points. Performance in numeracy increased the most (more than 40 score points) in Norway and Sweden. In Austria, Germany and the Slovak Republic, performance in numeracy increased by more than 35 points. In Canada*, France, Ireland*, Korea, New Zealand*, and the United Kingdom* (i.e. England and Northern Ireland*), performance in numeracy increased the least (fewer than 20 points).
In addition, data show the numeracy performance of the 10% lowest and 10% highest performers (OECD, 2021, p. 128[17]). The 10% lowest-achieving 15-year-olds had an average score of 211 on the PIAAC scale compared with a score of 235 for the 10% lowest-achieving 24-year-olds: an increase of 24 points. In contrast, the numeracy score of the 10% best-performing 15-year-olds was 326 compared to 355 for the 10% best-performing 24-year-olds: an increase of 28 points. These results suggest that, on average, the gap in performance between the highest and lowest achievers in numeracy increased.
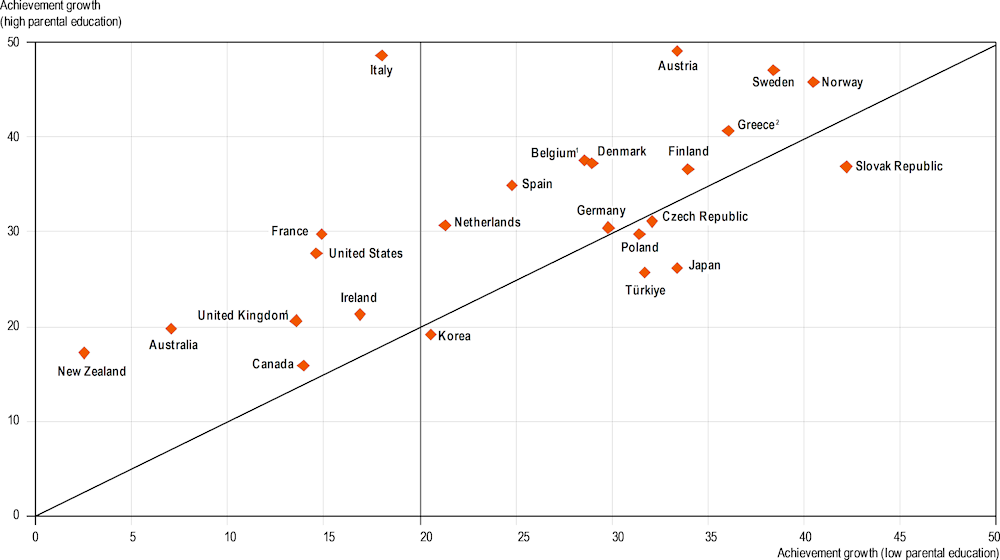
Figure I.2.8 shows the growth in numeracy skills between the ages of 15 and 24 in terms of students’ parents’ education level, which is used here as a proxy for socio-economic status. Results show that socio-economic inequalities not only persist but increase after leaving school in most countries with available data.
Figure I.2.8. Performance growth in numeracy between ages 15 and 24, by parental education
1. In PIAAC, data for Belgium refer only to Flanders and data for the United Kingdom* refer to England and Northern Ireland jointly.
2. The data for Greece include a large number of cases (1 032) in which there are responses to the background questionnaire but where responses to the assessment are missing. Proficiency scores have been estimated for these respondents based on their responses to the background questionnaire and the population model used to estimate plausible values for responses missing by design derived from the remaining 3 893 cases.
Notes: Only OECD countries with available information are shown. PIAAC data refers to 2012 except for Chile, Greece, Israel and New Zealand, which refer to 2015. PISA mathematics scores are expressed in PIAAC numeracy scores, following (Borgonovi et al., 2017[18]) and based on methods described in the OECD Skills Outlook 2021 (OECD, 2021[17]), Chapter 3, Box 3.1. Source: OECD Skills Outlook 2021 (OECD, 2021[17]), Table 3.15b.
On average across the 24 OECD countries represented in the figure, performance in numeracy increased by 25 score points among individuals whose parents had low levels of education (i.e. less than tertiary education completed) and by 32 points among individuals whose parents had high levels of education (i.e. tertiary education completed). Disparities in the growth of numeracy skills are marked in a number of countries, with the growth of skills especially high for individuals with highly educated parents. The vast majority of countries are in the upper triangle.
Policy implications
Once individuals leave compulsory education, their options for developing skills become very diverse. Some continue formal learning through adult education and training while others rely more on formal and informal learning at work and in everyday life. The impact of this differentiation on lifelong learning pathways can vary considerably between countries and within different groups within countries. An individual's ability to acquire new skills often depends on factors beyond the educational setting itself. Understanding what happens during this transition from school to young adulthood is essential. It is an opportunity for policy makers to promote foundational skills on a large scale and, where necessary, address educational deficits from earlier years.
Basic skills developed by age 15, including numeracy skills, are the foundation on which students develop their agency and transformative capacities (OECD, 2019[19]). While basic skills acquired early in school are perfected throughout life, the Skills Outlook 2021 shows the importance of acquiring a strong and solid foundation in school: data suggest that it is in the early years that essential skills are acquired and perfected.
1. The PIAAC numeracy scale that is used here has a mean of 263 and a standard deviation of 47. Thus, for example, the gain in young adulthood of 28 points from a baseline PIAAC score of 269 at age 15, represents about 60% of a standard deviation.
2. As discussed in Box 3.1, Chapter 3, of the OECD Skills Outlook 2021, in order to analyse literacy and numeracy performance growth between age 15 and young adulthood, analyses were conducted on synthetic cohorts, matching data from PISA and the relevant birth cohort in PIAAC: “Sample sizes used to construct the synthetic cohorts vary markedly: in PISA, the cohort comprises around 4 500 students per country, compared to only around 150 individuals in PIAAC. For this reason, the PIAAC age band was expanded to include people born one year before and after the relevant PISA cohort. For example, PISA 2000 results were matched to data for 26-28 year-olds surveyed in PIAAC in 2012 – which, unlike PISA, had been conducted only once so far – for the 17 countries that participated in both. To increase international coverage, data from PISA 2003 were added for three countries that administered PIAAC in 2015. Similarly, data for PISA 2003 were matched to data for 23-25 year-olds in PIAAC.” For further reference, see Annex Table 3.A.1 in the OECD Skills Outlook 2021.
Box I.2.3. The PISA 2022 framework for assessing mathematics
For the assessments of mathematics, reading and science, PISA develops subject-specific frameworks that define what it means to be proficient in the subject. These frameworks organise the subject according to key processes, contents and contexts that are measured in the assessment. The mathematics framework was updated for PISA 2022, while the reading and science frameworks remained identical to those used in 2018 (OECD, 2023[20]).
What’s new in the PISA 2022 mathematics framework
The new PISA 2022 mathematics framework considers that large-scale social changes such as digitalisation and new technologies; the ubiquity of data for making personal decisions; and the globalising economy have reshaped what it means to be mathematically competent and well-equipped to participate as a thoughtful, engaged, and reflective citizen in the 21st century. What these changes mean for education is that being mathematically proficient is less about the reproduction of routine procedures and more about the use of mathematical reasoning; that is, thinking mathematically in ways that allow students to solve increasingly complex real-life problems in a variety of 21st-century contexts.
Reasoning does not necessarily require employing advanced mathematics, it requires a clear understanding of basic (i.e. foundational) mathematical concepts. It is about thinking independently, logically, and creatively to approach real-world tasks that cannot be easily automatised or solved using simple “recipes”. Students at all levels of mathematics proficiency can demonstrate mathematical reasoning. At high levels of proficiency in mathematical reasoning, students understand that a problem is quantitative in nature and can formulate complex mathematical models to solve it. At lower levels of proficiency, mathematical reasoning is displayed by students who may not know much about formal mathematics but can intuitively spot a problem and solve it in informal ways, using elementary mathematics.
To develop students’ ability to reason mathematically, schools and education systems need to go beyond teaching and evaluating routine mathematical procedures – students need to be ready to address unfamiliar real-world problems and apply the mathematical tools they have in new ways.
Mathematical processes
For each of the four mathematical processes examined in PISA 2022, a mathematics subscale was developed. Each PISA mathematics test item is designed to capture one of the processes, and students are not necessarily expected to use all four to respond to each test item.
Mathematical reasoning: i.e. “thinking mathematically”, is the capacity to use mathematical concepts, tools, and logic to conceptualise and create solutions to real-life problems and situations. It involves recognising the mathematical nature inherent to a problem and developing strategies to solve it. This includes distinguishing between relevant and irrelevant information, using computational thinking, drawing logical conclusions, and recognising how solutions can be applied in a real-world context. Mathematical reasoning is also the capacity to construct arguments and provide evidence to support and explain ones’ answers and solutions, and to develop awareness of ones’ own thinking processes, including decisions made about which strategies to follow. Mathematical reasoning includes deductive and inductive reasoning. While reasoning underlies the other three mathematical processes described below, it nonetheless is different from them in that reasoning requires thinking through the whole problem-solving process rather than focusing on a specific part of it.
Formulating situations mathematically: mathematically literate students are able to recognise or identify the mathematical concepts and ideas underlying problems encountered in the real world, and then provide mathematical structure to the problems (i.e. formulate them in mathematical terms). This translation – from a contextualised situation to a well-defined mathematics problem – makes it possible to employ mathematical tools to solve real-world problems.
Employing mathematical concepts, facts and procedures: mathematically literate students are able to apply appropriate mathematics tools to solve mathematically formulated problems to obtain mathematical conclusions. This process involves activities such as performing arithmetic computations, solving equations, making logical deductions from mathematical assumptions, performing symbolic manipulations, extracting mathematical information from tables and graphs, representing and manipulating shapes in space, and analysing data.
Interpreting, applying, and evaluating mathematical outcomes: mathematically literate students are able to reflect upon mathematical solutions, results or conclusions and interpret them in the context of the real-life problem that started the process. This involves translating mathematical solutions or reasoning back into the context of the problem and determining whether the results are reasonable and make sense in the context of the problem.
Figure I.2.9. The mathematical modelling cycle in PISA 2022
Mathematical content
PISA 2022 developed a mathematics subscale for each of these four content domains:
Quantity: number sense and estimation; quantification of attributes, objects, relationships, situations and entities in the world; understanding various representations of those quantifications, and judging interpretations and arguments based on quantity.
Uncertainty and data: recognising the place of variation in the real world, including having a sense of the quantification of that variation, and acknowledging its uncertainty and error in related inferences. It also includes forming, interpreting and evaluating conclusions drawn in situations where uncertainty is present. The presentation and interpretation of data are also included in this category, as well as basic topics in probability.
Change and relationships: understanding fundamental types of change and recognising when they occur in order to use suitable mathematical models to describe and predict change. Includes appropriate functions and equations/inequalities as well as creating, interpreting and translating among symbolic and graphical representations of relationships.
Space and shape: patterns; properties of objects; spatial visualisations; positions and orientations; representations of objects; decoding and encoding of visual information; navigation and dynamic interaction with real shapes as well as representations, movement, displacement, and the ability to anticipate actions in space.
Real-world contexts
Mathematical reasoning and problem-solving take place in real-world contexts. There are four different contexts used in PISA 2022, which were also used in previous cycles:
Personal context: related to one’s self, one’s family or one’s peer group. For example, food preparation, shopping, games, personal health, personal transportation, recreation, sports, travel, personal scheduling and personal finance, etc.
Occupational context: related to the world of work. For example, measuring, costing and ordering materials for building payroll/accounting, quality control, scheduling/inventory, design/architecture and job-related decision making either with or without appropriate technology, etc.
Societal context: related to one’s community, whether local, national or global. For example, voting systems, public transport, government, public policies, demographics, advertising, health, entertainment, national statistics and economics, etc.
Scientific context: related to the application of mathematics to the natural world, and issues and topics related to science and technology. For example, weather or climate, ecology, medicine, space science, genetics, measurement and the world of mathematics itself
Descriptors of performance at the lower end of the mathematics scale
Drawing from the PISA for Development framework (OECD, 2018[21]), the six proficiency levels used in previous PISA mathematics assessments have been expanded. Specifically, Level 1 has now been expanded to include Level 1a, 1b and 1c (see Chapter 3 for a description of what students can do at each proficiency level in mathematics). Five test items measure Level 1b in the computer-based mathematics assessment, and one item measures Level 1c in the paper-based mathematics assessment.
Box I.2.4. How PISA measures reading and science skills
How PISA measures reading skills
In PISA 2022, reading proficiency is defined as follows: “Reading literacy is understanding, using, evaluating, reflecting on and engaging with texts in order to achieve one’s goals, to develop one’s knowledge and potential, and to participate in society” (OECD, 2019[22]).
PISA conceives of reading skills as a broad set of competencies that allows readers to engage with written information presented in one or more texts for a specific purpose (RAND Reading Study Group and Snow, 2022[23]; Perfetti, Landi and Oakhill, 2005[24]).
Readers must understand the text and integrate this with their pre-existing knowledge. They must examine the author’s (or authors’) point of view and decide whether the text is reliable and truthful, and whether it is relevant to their goals or purpose (Bråten, Strømsø and Britt, 2009[25]).
Reading in the 21st century involves not only the printed page but electronic formats (i.e. digital reading). It requires triangulating different sources, navigating through ambiguity, distinguishing between fact and opinion, and constructing knowledge. During the pandemic, remote teaching initiatives heavily relied on the availability of digital education resources.
The PISA reading framework developed in PISA 2018 was used again in PISA 2022.
How PISA measures science skills
As defined in PISA, scientific proficiency is the ability to engage with science-related issues and the ideas of science as a reflective citizen (OECD, 2019[22]). A scientifically proficient person, therefore, is willing to engage in reasoned discourse about science and technology, which requires the competencies of:
Explaining phenomena scientifically: recognising, offering, and evaluating explanations for a range of natural and technological phenomena.
Evaluating and designing scientific enquiry: describing and appraising scientific investigations and proposing ways of addressing questions scientifically.
Interpreting data and evidence scientifically: analysing and evaluating data, claims and arguments in a variety of representations and drawing appropriate scientific conclusions.
Within this framework, performance in science requires three forms of knowledge: content knowledge, knowledge of the standard methodological procedures used in science, and knowledge of the reasons and ideas used by scientists to justify their claims. Explaining scientific and technological phenomena, for instance, demands knowledge of the content of science. Evaluating scientific enquiry and interpreting evidence scientifically also require an understanding of how scientific knowledge is established and the degree of confidence with which it is held. Therefore, individuals who are scientifically literate understand the major concepts and ideas that form the foundation of scientific and technological thought; how such knowledge has been derived; and the degree to which such knowledge is justified by evidence or theoretical explanations.
The definition of science proficiency recognises that there is an affective element to a student’s competency: students’ attitudes or dispositions towards science can influence their level of interest, sustain their engagement and motivate them to take action.
Science was the major assessment subject in PISA 2006 and 2015. The science assessment was updated in 2015 and was used again in PISA 2018 and PISA 2022. The PISA science framework developed in PISA 2015 continued to be used in PISA 2018 and PISA 2022.
Table I.2.9. How did countries perform in PISA 2022? Chapter 2 figures and tables
|
Table I.2.1 |
Comparing countries’ and economies’ performance in mathematics |
|
Table I.2.2 |
Comparing countries’ and economies’ performance in reading |
|
Table I.2.3 |
Comparing countries’ and economies’ performance in science |
|
Figure I.2.1 |
Mathematics anxiety and mean score in mathematics in PISA 2022 |
|
Figure I.2.2 |
Mathematics performance and anxiety in mathematics among students with fixed and growth mindsets |
|
Figure I.2.3 |
Average performance in mathematics and variation in performance |
|
Figure I.2.4 |
Mean score in mathematics at 10th, 50th and 90th percentile of performance distribution |
|
Figure I.2.5 |
Variation in mathematics performance between systems, schools and students |
|
Figure I.2.6 |
Variation in mathematics performance between and within schools |
|
Table I.2.4 |
Mathematics performance at national and subnational levels |
|
Table I.2.5 |
Reading performance at national and subnational levels |
|
Table I.2.6 |
Science performance at national and subnational levels |
|
Table I.2.7 |
Comparing countries and economies on the mathematics-process subscales |
|
Table I.2.8 |
Comparing countries and economies on the mathematics-content subscales |
|
Figure I.2.7 |
Performance growth in numeracy between ages 15 and 24 |
|
Figure I.2.8 |
Performance growth in numeracy between ages 15 and 24, by parental education |
|
Figure I.2.9 |
The mathematical modelling cycle in PISA 2022 |
References
[6] Ashcraft, M. and E. Kirk (2001), “The relationships among working memory, math anxiety, and performance.”, Journal of Experimental Psychology: General, Vol. 130/2, pp. 224-237, https://doi.org/10.1037/0096-3445.130.2.224.
[16] Beilock, S. et al. (2010), “Female teachers’ math anxiety affects girls’ math achievement”, Proceedings of the National Academy of Sciences, Vol. 107/5, pp. 1860-1863, https://doi.org/10.1073/pnas.0910967107.
[18] Borgonovi, F. et al. (2017), Youth in Transition: How Do Some of The Cohorts Participating in PISA Fare in PIAAC?, OECD Publishing, https://doi.org/10.1787/51479ec2-en.
[25] Bråten, I., H. Strømsø and M. Britt (2009), “Trust Matters: Examining the Role of Source Evaluation in Students’ Construction of Meaning Within and Across Multiple Texts”, Reading Research Quarterly, Vol. 44/1, pp. 6-28, https://doi.org/10.1598/rrq.44.1.1.
[4] Carey, E. et al. (2016), “The Chicken or the Egg? The Direction of the Relationship Between Mathematics Anxiety and Mathematics Performance”, Frontiers in Psychology, Vol. 6, https://doi.org/10.3389/fpsyg.2015.01987.
[2] Choe, K. et al. (2019), “Calculated avoidance: Math anxiety predicts math avoidance in effort-based decision-making”, Science Advances, Vol. 5/11, https://doi.org/10.1126/sciadv.aay1062.
[3] Dowker, A., A. Sarkar and C. Looi (2016), “Mathematics Anxiety: What Have We Learned in 60 Years?”, Frontiers in Psychology, Vol. 7, https://doi.org/10.3389/fpsyg.2016.00508.
[14] Dweck, C. (2006), Mindset: The new psychology of success, Random House.
[15] Dweck, C. and D. Yeager (2019), “Mindsets: A View From Two Eras”, Perspectives on Psychological Science, Vol. 14/3, pp. 481-496, https://doi.org/10.1177/1745691618804166.
[7] Elliot, A. and C. Dweck (eds.) (2005), Evaluation anxiety, The Guilford Press.
[5] Goetz, T. et al. (2010), “Academic self-concept and emotion relations: Domain specificity and age effects”, Contemporary Educational Psychology, Vol. 35/1, pp. 44-58, https://doi.org/10.1016/j.cedpsych.2009.10.001.
[9] Ho, H. et al. (2000), “The Affective and Cognitive Dimensions of Math Anxiety: A Cross-National Study”, Journal for Research in Mathematics Education, Vol. 31/3, pp. 362-379, https://doi.org/10.2307/749811.
[20] OECD (2023), PISA 2022 Assessment and Analytical Framework, PISA, OECD Publishing, Paris, https://doi.org/10.1787/dfe0bf9c-en.
[17] OECD (2021), OECD Skills Outlook 2021: Learning for Life, OECD Publishing, Paris, https://doi.org/10.1787/0ae365b4-en.
[12] OECD (2021), Sky’s the limit: growth mindset, students, and schools in PISA, OECD publishing, Paris.
[19] OECD (2019), OECD Future of Education and Skills 2030 Concept Note.
[22] OECD (2019), PISA 2018 Assessment and Analytical Framework, PISA, OECD Publishing, Paris, https://doi.org/10.1787/b25efab8-en.
[21] OECD (2018), PISA for Development Assessment and Analytical Framework: Reading, Mathematics and Science, PISA, OECD Publishing, Paris, https://doi.org/10.1787/9789264305274-en.
[1] OECD (2013), PISA 2012 Results: Ready to Learn (Volume III): Students’ Engagement, Drive and Self-Beliefs, PISA, OECD Publishing, Paris, https://doi.org/10.1787/9789264201170-en.
[24] Perfetti, C., N. Landi and J. Oakhill (2005), “The Acquisition of Reading Comprehension Skill”, in The Science of Reading: A Handbook, Blackwell Publishing Ltd, Oxford, UK, https://doi.org/10.1002/9780470757642.ch13.
[8] Putwain, D., K. Woods and W. Symes (2010), Personal and situational predictors of test anxiety of students in post-compulsory education.
[23] RAND Reading Study Group and C. Snow (2022), Reading for Understanding: Toward an R&D Program in Reading Comprehension, RAND Corporation, http://www.jstor.org/stable/10.7249/mr1465oeri.8.
[13] Yeager, D. et al. (2019), A national experiment reveals where a growth mindset improves achievement, https://doi.org/10.1038/s41586-019-1466-y.
[11] Yeager, D. and G. Walton (2011), Social-psychological interventions in education: They’re not magic, SAGE Publications Inc., http://rer.aera.net.
[10] Zhang, J., N. Zhao and Q. Kong (2019), “The Relationship Between Math Anxiety and Math Performance: A Meta-Analytic Investigation”, Frontiers in Psychology, Vol. 10, https://doi.org/10.3389/fpsyg.2019.01613.
Notes
← 1. When comparing mean performance across countries/economies, only differences that are statistically significant should be considered (see Box 1 in Reader’s Guide).
← 2. The standard deviation summarises variation in performance among 15-year-old students within each country/economy. The average standard deviation in mathematics performance within OECD countries is 90 score points. If the standard deviation is larger than 90 score points, it indicates that student performance varies more from a particular country’s/economy’s average performance than it varies internationally. A smaller standard deviation means that student performance varies less in a country/economy than it varies internationally.
← 3. This analysis was carried out in two steps. In the first step, the share of the variation in student performance that occurs between education systems was identified. In the second step, out of the remaining variation, the between-school and within-school was identified. Within-school variation are differences in performance between students.
← 4. PISA results do not establish causality. PISA identifies empirical correlations between student achievement and the characteristics of schools and education systems, correlations that show consistent patterns across countries. Implications for policy are based on this correlational evidence and previous research.
← 5. The reason for this restriction is the following: while the students sampled in PISA represent all 15-year-old students, whatever type of school they are enrolled in, they may not be representative of the students enrolled in their school. As a result, comparability at the school level may be compromised. For example, if grade repeaters in a country are enrolled in different schools than students in the modal grade because the modal grade in this country is the first year of upper secondary school (ISCED 3) while grade repeaters are enrolled in lower secondary school (ISCED 2), the average performance of schools where only students who had repeated a grade were assessed may be a poor indicator of the actual average performance of these schools. By restricting the sampling to schools with the modal ISCED level for 15-year-old students, PISA ensures that the characteristics of the students sampled are as close as possible to the profiles of the students attending the school. The “modal ISCED level” is defined here as the level attended by at least one-third of the PISA sample. In 15 education systems (Baku [Azerbaijan], Cambodia, Colombia, Costa Rica, the Czech Republic, the Dominican Republic, Hong Kong [China]*, Indonesia, Jamaica, Kazakhstan, Morocco, the Netherlands, the Slovak Republic, Switzerland, and Chinese Taipei) both lower secondary (ISCED level 2) and upper secondary (ISCED level 3) schools meet this definition. In all other countries, analyses are restricted to either lower secondary or upper secondary schools (see Table I.B1.2.14 for details). In several countries, lower and upper secondary education are provided in the same school. As the restriction is made at the school level, some students from a grade other than the modal grade in the country may also be used in the analysis.
← 6. See Annex A3 for a technical note on how the range of ranks were computed in PISA 2022.