Résultats de TALIS 2018 (Volume II)

Annex B. Notes techniques sur les analyses du présent volume

Utilisation des pondérations pour les enseignants et les établissements

Les statistiques présentées dans ce rapport sont tirées de données obtenues à partir d’échantillons d’établissements, de chefs d’établissement et d’enseignants. L’échantillon a été prélevé selon une méthode d’échantillonnage aléatoire stratifié à deux degrés. En d’autres termes, les enseignants (unités d’échantillonnage du second degré ou secondaires) ont été choisis au hasard dans la liste des enseignants couverts par le champ d’application pour chacun des établissements choisis au hasard (unités d’échantillonnage du premier degré ou primaire). Pour que ces statistiques soient pertinentes pour un pays, elles doivent refléter l’ensemble de la population dont elles sont tirées et pas seulement l’échantillon utilisé pour les collecter. D’où la nécessité d’utiliser des pondérations d’enquête afin d’obtenir des estimations non biaisées des paramètres de la population ou du modèle.

Les pondérations finales permettent de produire des estimations au niveau des pays à partir des données d’échantillonnage observées. La pondération de l’estimation indique combien d’unités de population sont représentées par unité échantillonnée. La pondération finale est la combinaison de plusieurs facteurs reflétant les probabilités de sélection aux différentes étapes de l’échantillonnage et la réponse obtenue à chaque étape. D’autres facteurs peuvent également entrer en ligne de compte en fonction des conditions particulières qui permettent d’assurer l’impartialité des estimations (p. ex. un ajustement pour les enseignants travaillant dans plus d’un établissement).

Les statistiques présentées dans ce rapport, fondées sur les réponses des chefs d’établissement qui contribuent aux estimations relatives aux chefs d’établissement, ont été estimées à l’aide des pondérations des établissements (SCHWGT). Les résultats fondés uniquement sur les réponses des enseignants ou sur les réponses des enseignants et des chefs d’établissement (c.-à-d. la fusion des réponses des chefs d’établissement avec celles des enseignants) ont été pondérés en fonction de la pondération des enseignants (TCHWGT).

Utilisation de variables et d’échelles complexes

Échelles

Dans le présent rapport, plusieurs indices d’échelle sont utilisés dans les analyses de régression. Les descriptions de l’établissement et de la validation de ces échelles sont disponibles dans le chapitre 11 du rapport TALIS 2018 Technical Report (OCDE, 2019_[1]).

Ratios et autres variables dérivés des données de l’Enquête TALIS

Ratio entre le nombre d’enseignants ayant définitivement quitté l’établissement dans les 12 mois précédant l’Enquête ou absents depuis le mardi précédant l’Enquête et l’effectif total d’enseignants de cet établissement – Dans l’Enquête TALIS 2018, les indicateurs de l’absentéisme et du renouvellement des enseignants sont dérivés des réponses des chefs d’établissement à des items sur le nombre d’enseignants (à temps plein et à temps partiel) absents depuis le dernier mardi de la période scolaire et sur le nombre d’enseignants qui ont quitté l’établissement définitivement au cours des 12 mois précédant l’Enquête. Les quatre options de réponse à ces questions sont : « 0 » ; « 1-5 » ; « 6-10 » ; « 11-15 » ; et « 16 ou plus ». Le nombre d’enseignants absents et ayant quitté définitivement leur établissement communiqué par les chefs d’établissement a été recodé en fonction de la limite inférieure de chaque option de réponse, soit « 0 » ; « 1 » ; « 6 » ; « 11 » ; et « 16 ». Les indicateurs sur l’absentéisme et le renouvellement des enseignants ont été estimés en fonction du rapport entre le nombre d’enseignants absents de leur établissement ou l’ayant quitté définitivement et l’effectif total des enseignants de cet établissement. Le tableau du chapitre 2 où ce ratio est indiqué a été élaboré au niveau de l’établissement et, donc, en s’appuyant sur les coefficients de pondération des établissements (SCHWGT). Toutefois, un ratio dérivé d’un indicateur catégoriel (le nombre d’enseignants absents de leur établissement ou l’ayant quitté définitivement, selon leur chef d’établissement) et d’un indicateur continu (l’effectif total d’enseignants) est difficile à interpréter, car il dépend fortement de la taille des établissements. C’est la raison pour laquelle les chiffres relatifs à l’absentéisme et au renouvellement des enseignants ne sont pas présentés dans le corps du texte, mais uniquement dans les tableaux II.2.59 et II.2.60.

Responsabilité globale des chefs d’établissement – Les analyses du chapitre 5 sur la part de responsabilité des chefs d’établissement dans des décisions relatives à leur établissement se basent sur les réponses des chefs d’établissement à une question les invitant à indiquer les personnes ou entités ayant un pouvoir considérable de décision dans un certain nombre de domaines. Les chefs d’établissement on répondu aux affirmations par « oui » ou « non », afin d’indiquer s’il s’agit : du chef d’établissement, d’autres membres de l’équipe de direction, des enseignants, du conseil d’administration de l’établissement ou des autorités locales.

L’indice a été créé selon une technique simple de catégorisation. Si le chef d’établissement a indiqué :

• qu’il a un pouvoir considérable dans une majorité des décisions, il est réputé avoir une grande part de responsabilité dans son établissement

• qu’il a un pouvoir considérable dans une minorité des décisions, il est réputé ne pas avoir une grande part de responsabilité dans son établissement

• qu’il a un pouvoir considérable dans une moitié des décisions, les observations correspondantes ont été exclues de l’indice.

Les items retenus pour constituer l’indice sont les suivants :

• Autonomie des établissements en matière de personnel

  • recrutement ou embauche des enseignants

  • licenciement ou suspension des enseignants

• Autonomie des établissements en matière de budget

  • fixation du salaire de départ des enseignants, y compris les grilles salariales

  • détermination des augmentations de salaire des enseignants

  • décision sur la répartition du budget dans l’établissement

• Autonomie des établissements en matière pédagogique

  • définition du règlement intérieur à respecter par les élèves

  • définition des politiques d’évaluation des élèves

  • approbation des admissions des élèves dans l’établissement

  • choix du matériel pédagogique à utiliser

  • choix du contenu des cours, y compris les évaluations nationales/régionales

  • choix des cours à offrir

Les catégories de l’indice sont 1 (« pouvoir considérable ») et 0 (« pas de pouvoir considérable »).

Responsabilité globale des enseignants en matière pédagogique – Les analyses du chapitre 5 sur la part de responsabilité des enseignants dans des décisions pédagogiques dans leur établissement se basent sur les réponses des chefs d’établissement à une question les invitant à indiquer les personnes ou entités ayant un pouvoir considérable de décision dans un certain nombre de domaines. Les chefs d’établissement ont répondu « oui » ou « non », afin d’indiquer s’il s’agit : du chef d’établissement, d’autres membres de l’équipe de direction, des enseignants, du conseil d’administration de l’établissement ou des autorités locales.

L’indice a été créé selon une technique simple de catégorisation. Si le chef d’établissement a indiqué :

• que les enseignants ont un pouvoir considérable dans une majorité des décisions, ils sont réputés avoir une grande part de responsabilité dans leur établissement

• que les enseignants ont un pouvoir considérable dans une minorité des décisions, ils sont réputés ne pas avoir une grande part de responsabilité dans leur établissement

• que les enseignants ont un pouvoir considérable dans une moitié des décisions, les observations correspondantes ont été exclues de l’indice.

Les items retenus pour constituer l’indice sont les suivants :

• Autonomie des établissements en matière pédagogique

  • définition du règlement intérieur à respecter par les élèves

  • définition des politiques d’évaluation des élèves, y compris des évaluations nationales/régionales

  • approbation des admissions des élèves dans l’établissement

  • choix du matériel pédagogique à utiliser

  • choix du contenu des cours, y compris dans les programmes nationaux/régionaux

  • choix des cours à offrir

Les catégories de l’indice sont 1 (« pouvoir considérable ») et 0 (« pas de pouvoir considérable »).

Moyennes internationales

Les moyennes de l’OCDE et de TALIS, calculées pour la plupart des indicateurs présentés dans ce rapport, correspondent à la moyenne arithmétique des estimations nationales respectives. Lorsque les statistiques sont basées sur les réponses des enseignants, les moyennes de l’OCDE et de TALIS couvrent respectivement 31 et 48 pays et économies (tableau AII.B.1). Dans les cas où l’analyse est fondée sur les réponses des chefs d’établissement, les moyennes de l’OCDE et de TALIS couvrent, respectivement, 30 et 47 pays et économies.

Tableau AII.B.1. Moyenne internationale des pays couverts dans le rapport TALIS 2018

	Moyenne TALIS-48 (enseignants)	Moyenne TALIS-47 (chefs d’établissement)	Moyenne OCDE-31 (enseignants)	Moyenne OCDE-30 (chefs d’établissement)	Total UE-23
Alberta (Canada)	x	x	x	x	–
Australie	x	–	x	–	–
Autriche	x	x	x	x	x
Belgique	x	x	x	x	x
Comm. flamande (Belgique)	–	–	–	–	–
Comm. Française (Belgique)	–	–	–	–	–
Brésil	x	x	–	–	–
Bulgarie	x	x	–	–	x
CABA (Argentine)*	x	x	–	–	–
Chili	x	x	x	x	–
Colombie1	x	x	x	x	–
Croatie	x	x	–	–	x
Chypre	x	x	–	–	x
République tchèque	x	x	x	x	x
Danemark	x	x	x	x	x
Angleterre (RU)	x	x	x	x	x
Estonie	x	x	x	x	x
Finlande	x	x	x	x	x
France	x	x	x	x	x
Géorgie	x	x	–	–	–
Hongrie	x	x	x	x	x
Islande	x	x	x	x	–
Israël	x	x	x	x	–
Italie	x	x	x	x	x
Japon	x	x	x	x	–
Kazakhstan	x	x	–	–	–
Corée	x	x	x	x	–
Lettonie	x	x	x	x	x
Lituanie	x	x	x	x	x
Malte	x	x	–	–	x
Mexique	x	x	x	x	–
Pays-Bas	x	x	x	x	x
Nouvelle-Zélande	x	x	x	x	–
Norvège	x	x	x	x	–
Portugal	x	x	x	x	x
Roumanie	x	x	–	–	x
Fédération de Russie	x	x	–	–	–
Arabie saoudite	x	x	–	–	–
Shanghai (Chine)	x	x	–	–	–
Singapour	x	x	–	–	–
République slovaque	x	x	x	x	x
Slovénie	x	x	x	x	x
Afrique du Sud	x	x	–	–	–
Espagne	x	x	x	x	x
Suède	x	x	x	x	x
Taipei chinois	x	x	–	–	–
Turquie	x	x	x	x	–
Émirats arabes unis	x	x	–	–	–
États-Unis	x	x	x	x	–
Viet Nam	x	x	–	–	–

* CABA (Argentine) : Ciudad Autónoma de Buenos Aires, Argentine.

1. Le 25 mai 2018, le Conseil de l’OCDE a invité la Colombie à devenir membre. Bien que la Colombie figure dans les moyennes de l’OCDE reportées dans cette publication, au moment de sa préparation, elle était sur le point d’achever ses procédures internes de ratification et le dépôt de son instrument d’adhésion à la Convention de l’OCDE était en suspens.

Le total UE représente les 23 États membres de l’Union européenne qui ont également participé à l’Enquête TALIS 2018 en tant qu’entité unique et à laquelle chacun des 23 États membres de l’UE contribue proportionnellement au nombre d’enseignants ou de chefs d’établissement, en fonction de l’analyse réalisée. Le total UE est donc calculé sous la forme d’une moyenne arithmétique pondérée basée sur la somme des pondérations finales des enseignants (TCHWGT) ou des chefs d’établissement (SCHWGT) par pays, en fonction de la population cible.

Dans la présente publication, la moyenne de l’OCDE est généralement utilisée lorsqu’on veut mettre l’accent sur une tendance globale pour un indicateur et sur la comparaison de ses valeurs entre systèmes éducatifs. Dans le cas de certains pays et économies, les données peuvent ne pas être disponibles pour des indicateurs spécifiques, ou des catégories spécifiques peuvent ne pas s’appliquer. Par conséquent, les lecteurs doivent garder à l’esprit que le terme « moyenne de l’OCDE » fait référence aux pays et économies de l’OCDE inclus dans les comparaisons respectives. Dans les cas où les données ne sont pas disponibles ou ne s’appliquent pas à toutes les sous-catégories d’une population ou d’un indicateur donné, la « moyenne de l’OCDE » peut être cohérente dans chaque colonne d’un tableau, mais pas nécessairement dans toutes les colonnes d’un tableau.

Erreurs-types et tests de signification

Les statistiques présentées dans le présent rapport constituent des estimations fondées sur des échantillons d’enseignants et de chefs d’établissement, plutôt que des valeurs qui auraient pu être calculées si chaque enseignant et chaque chef d’établissement dans chaque pays avaient répondu à chaque question. D’où l’importance d’évaluer le degré d’incertitude des estimations. Dans l’Enquête TALIS, chaque estimation est associée à un degré d’incertitude exprimé en erreur-type. L’utilisation d’intervalles de confiance permet de tirer des conclusions sur les moyennes et les proportions de la population d’une manière qui reflète l’incertitude associée aux estimations de l’échantillon. À partir d’une statistique de l’échantillon observée et en présumant une distribution normale, on peut déduire que le résultat obtenu se situera dans l’intervalle de confiance dans 95 répétitions sur 100 de la mesure sur différents échantillons prélevés à partir de la même population. Les erreurs-types signalées ont été calculées à l’aide d’une méthode de répétition compensée (BRR).

Différences entre les sous-groupes

Les différences entre les sous-groupes d’enseignants (par exemple, les enseignantes et les enseignants) et les caractéristiques des établissements (par exemple, les établissements ayant une forte concentration d’élèves issus de milieux socio-économiques défavorisés et ceux ayant une faible concentration d’élèves issus de milieux socio-économiques défavorisés) ont été testées pour déterminer leur signification statistique. Toutes les différences indiquées en gras dans les tableaux de données du présent rapport sont significativement différentes d’un point de vue statistique de 0 à un niveau de confiance de 95 %.

En cas de différences entre sous-groupes, l’erreur-type est calculée en tenant compte du fait que les deux sous-échantillons ne sont pas indépendants. Par conséquent, la valeur attendue de la covariance peut différer de 0, ce qui mène à des estimations moindres de l’erreur-type comparativement aux estimations de l’erreur-type pour une différence entre sous-échantillons indépendants.

La répartition des enseignants et des établissements par caractéristique est présentée dans les tableaux AII.B.3, AII.B.4, AII.B.5 et AII.B.6. de l’annexe C.

Différences entre les cycles

La signification statistique des différences entre les cycles TALIS (p. ex. évolution entre 2013 et 2018) a été testée. Toutes les différences indiquées en gras dans les tableaux de données du présent rapport sont statistiquement significatives au niveau de 95 %. Étant donné que les échantillons de différents cycles de TALIS sont considérés comme indépendants, l’erreur-type pour toute comparaison entre cycles est calculée avec une valeur escomptée de la covariance égale à 0.

Statistiques basées sur les régressions

Une analyse de régression a été effectuée pour explorer les relations entre les différentes variables. La régression linéaire multiple a été utilisée dans les cas où la variable dépendante (ou de résultat) était considérée comme continue. La régression logistique binaire a été utilisée lorsque la variable dépendante (ou résultat) était catégorielle binaire. Des analyses de régression ont été effectuées pour chaque pays séparément. À l’instar des autres statistiques présentées dans ce rapport, les moyennes de l’OCDE et de TALIS se réfèrent à la moyenne arithmétique des estimations au niveau des pays, tandis que le total UE est calculé comme une moyenne arithmétique pondérée basée sur la somme des pondérations finales des enseignants (TCHWGT) ou des chefs d’établissement (SCHWGT) par pays, selon la population cible.

Les variables de contrôle incluses dans un modèle de régression sont choisies en fonction d’un raisonnement théorique et, de préférence, limitées aux mesures les plus objectives ou à celles qui ne changent pas avec le temps. Le contrôle des caractéristiques des enseignants comprend le sexe, l’âge, le statut professionnel (c.-à-d. temps plein ou temps partiel) et le nombre d’années d’expérience dans l’enseignement. Le contrôle des caractéristiques des classes comprend : les variables de la composition de la classe (c.-à-d. la proportion d’élèves dont la langue maternelle est différente de la langue d’enseignement, les élèves peu performants, les élèves ayant des besoins spécifiques d’éducation, les élèves ayant des problèmes de comportement, les élèves issus de milieux socio-économiques défavorisés, les élèves très doués, les élèves immigrés ou issus de l’immigration, les élèves réfugiés) et la taille des classes.

Dans le cas des modèles de régression fondés sur la régression linéaire multiple, le pouvoir explicatif des modèles de régression est également mis en évidence par le R au carré (R2), qui représente la proportion de la variation observée de la variable dépendante (ou résultat) qui peut être expliquée par les variables indépendantes (ou explicatives).

Afin d’assurer la robustesse des modèles de régression, des variables indépendantes ont été introduites par étapes dans les modèles. Cette approche exigeait également que les modèles à chaque étape soient fondés sur le même échantillon. L’échantillon restreint utilisé pour les différentes versions du même modèle correspondait à l’échantillon de la version la plus étendue (c’est-à-dire avec le nombre maximum de variables indépendantes) du modèle. L’échantillon restreint de chaque modèle de régression excluait donc ces observations lorsque toutes les variables indépendantes avaient des valeurs manquantes.

Analyse de régression linéaire multiple

L’analyse de régression linéaire multiple donne un aperçu de la façon dont la valeur de la variable dépendante continue (ou de résultat) change lorsque l’une des variables indépendantes (ou explicatives) varie alors que toutes les autres variables indépendantes restent constantes. En général, et toutes choses étant égales par ailleurs, une augmentation d’une unité de la variable indépendante (X_i) augmente, en moyenne, la variable dépendante (Y) des unités représentées par le coefficient de régression (β_i) :

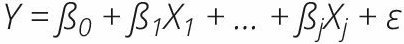
En interprétant les coefficients de régression multiples, il est important de garder à l’esprit que chaque coefficient est influencé par les autres variables indépendantes dans un modèle de régression. L’influence dépend du degré de corrélation entre les variables indépendantes. Par conséquent, chaque coefficient de régression ne rend pas compte de l’effet total des variables indépendantes sur les variables dépendantes. Chaque coefficient représente plutôt l’effet additionnel de l’ajout de cette variable au modèle, si les effets de toutes les autres variables du modèle sont déjà pris en compte. Il est également important de noter que, puisque des données d’enquêtes transversales ont été utilisées dans ces analyses, on ne peut tirer aucune conclusion de type causal.

Les coefficients de régression en gras dans les tableaux de données présentant les résultats de l’analyse de régression sont significativement différents d’un point de vue statistique de 0 à un niveau de confiance de 95 %.

Analyse de régression logistique binaire

L’analyse de régression logistique binaire permet d’estimer la relation entre une ou plusieurs variables indépendantes (ou explicatives) et la variable dépendante (ou de résultat) avec deux catégories. Le coefficient de régression (ß) d’une régression logistique est l’augmentation estimée de la cote logarithmique du résultat par unité d’augmentation de la valeur de la variable prédictive.

De façon plus formelle, soit Y la variable binaire de résultat indiquant non/oui avec 0/1, et p la probabilité que Y soit 1, de sorte que p = prob (Y=1). Soit X₁,… X_k est un ensemble de variables explicatives. Alors, la régression logistique de Y sur X₁,… X_k estime les valeurs des paramètres pour ß₀, ß₁,..., ß_k par la méthode du maximum de vraisemblance de l’équation suivante :

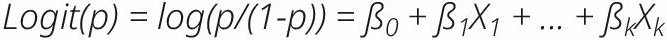
De plus, on obtient la fonction exponentielle du coefficient de régression (exp (ß)), qui est le rapport de cotes (RC) associé à une augmentation d’une unité dans la variable explicative. Ensuite, en termes de probabilités, l’équation ci-dessus se traduit comme suit :

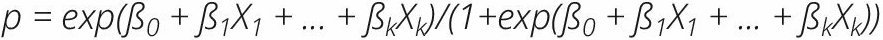
La transformation des cotes logarithmiques (ß) en rapports de cotes (exp (ß) ; RC) permet de mieux interpréter les données en termes de probabilité. Le rapport de cotes (RC) est une mesure de la probabilité relative d’un résultat particulier dans deux groupes. Le rapport de cotes pour l’observation du résultat en cas de présence d’un antécédent est :

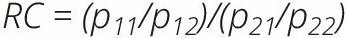
où p₁₁/p₁₂ représente la « probabilité » d’observer le résultat lorsque l’antécédent est présent, et p21/p22 représente la « probabilité » d’observer le résultat lorsque l’antécédent est absent. Ainsi, un rapport de cotes indique dans quelle mesure une variable explicative est associée à une variable de résultat catégorique comportant deux catégories (p. ex. oui/non) ou plus. Un rapport de cotes inférieur à 1 dénote une association négative ; un rapport de cotes supérieur à 1 indique une association positive ; et un rapport de cotes égal à 1 signifie qu’il n’y a pas d’association. Par exemple, si on analyse l’association entre le fait d’être une enseignante et le fait d’avoir fait de l’enseignement son premier choix de carrière, les rapports de cotes suivants seraient interprétés comme suit :

• 0.2 : Les enseignantes sont cinq fois moins susceptibles que les enseignants d’avoir fait de l’enseignement leur premier choix de carrière.

• 0.5 : Les enseignantes sont deux fois moins susceptibles que les enseignants d’avoir fait de l’enseignement leur premier choix de carrière.

• 0.9 : Les enseignantes sont 10 % moins susceptibles que les enseignants d’avoir fait de l’enseignement leur premier choix de carrière.

• 1 : Les enseignantes et enseignants sont tout autant susceptibles d’avoir fait de l’enseignement leur premier choix de carrière.

• 1.1 : Les enseignantes sont 10 % plus susceptibles d’avoir fait de l’enseignement leur premier choix de carrière que les enseignants.

• 2 : Les enseignantes sont deux fois plus susceptibles que les enseignants d’avoir fait de l’enseignement leur premier choix de carrière.

• 5 : Les enseignantes sont cinq fois plus susceptibles que les enseignants d’avoir fait de l’enseignement leur premier choix de carrière.

Les rapports de cotes sont en gras si le ratio relatif risque/cote est différent de 1 dans une mesure statistiquement significative à un niveau de confiance de 95 %. La signification statistique autour de 1 (hypothèse nulle) est calculé dans le scénario où la statistique du rapport risque/ratio relatif suit une distribution log-normale et non une distribution normale, selon l’hypothèse nulle.

Dans les modèles logistiques des tableaux II.2.53, II.2.54, II.2.55 et II.2.56 du chapitre 2, la probabilité que les enseignants souffrent « dans une grande mesure » de stress professionnel (variable binaire) varie en fonction de l’intensité (exprimée en nombre d’heures) de tâches spécifiques (variable explicative continue) et de leurs termes quadratiques, ajoutés pour tenir compte des cas possibles de non-linéarité.

Une fois estimés, les coefficients des modèles logistiques sont convertis en probabilité comme suit :

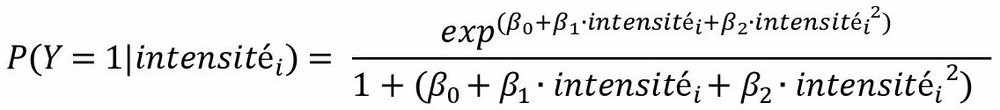
Où

• P(Y=1|intensité) est la probabilité de souffrir « dans une grande mesure » de stress professionnel compte tenu du nombre d’heures (intensité) consacré à la tâche i (enseignement, planification ou préparation des cours, correction des copies des élèves et travail administratif d’ordre général) ;

• β₀, β₁, β₂ sont les coefficients du modèle logistique et, l’intercept.

Enfin, la probabilité de souffrir « dans une grande mesure » de stress professionnel associée à une intensité des tâches donnée est multipliée par 100 pour estimer le pourcentage d’enseignants souffrant de stress au travail « dans une grande mesure » à cette intensité.

Statistiques basées sur des modèles multiniveaux : coefficient de corrélation intra-classe

Les statistiques basées sur des modèles multiniveaux qui sont présentées aux chapitres 2 et 4 comportent des composantes de la variance (variance inter-établissements et intra-établissement) dont est dérivé le coefficient de corrélation intra-classe. Les modèles multiniveaux sont des régressions à deux niveaux (le niveau « enseignant » et le niveau « établissement), avec distribution normale des résidus et sont estimés selon la méthode de la probabilité maximale. Les modèles sont estimés selon le module « mixte » Stata (version 15.1).

Le coefficient de corrélation intra-classe correspond à la part de la variance située dans les établissements ; il se définit et s’estime comme suit :

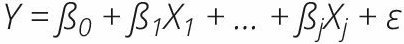
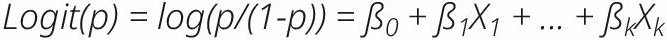
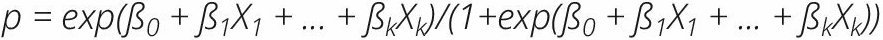
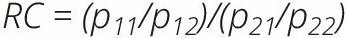
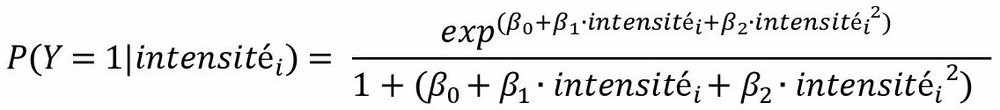
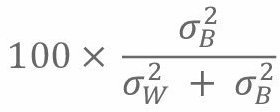
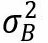Où et 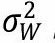, sont respectivement la variance inter-établissements et intra-établissement estimée.

Erreurs-types dans les estimations dérivées de modèles multiniveaux

Dans les statistiques dérivées de modèles multiniveaux, telles que les estimations des composantes de la variance, les erreurs-types ne sont pas calculées selon la méthode habituelle de la réplication, qui tient compte des taux d’échantillonnage et de la stratification des populations finies. Les erreurs-types sont calculées sur la base des modèles dans l’hypothèse que l’échantillon d’établissements et d’enseignants parmi ceux qui y sont en poste est prélevé de manière aléatoire (les probabilités d’échantillonnage étant indiquées dans le coefficient de pondération des établissements et des enseignants) dans une population infinie, théorique, d’établissements et d’enseignants, qui correspond aux hypothèses paramétriques des modèles. L’erreur-type de l’indice d’inclusion estimé est dérivée d’une distribution approximative des erreurs-types (basées sur les modèles) des composantes de la variance selon la méthode delta.

Coefficient de corrélation de Pearson

Le coefficient de corrélation mesure la force et la direction de l’association statistique entre deux variables. Les coefficients de corrélation varient entre -1 et 1 ; les valeurs autour de 0 indiquent une faible association, tandis que les valeurs extrêmes indiquent l’association négative ou positive la plus forte possible. Le coefficient de corrélation de Pearson (indiqué par la lettre r) mesure la force et la direction de la relation linéaire entre deux variables.

Dans le présent rapport, les coefficients de corrélation de Pearson quantifient les relations entre les statistiques nationales.

Changements entre les cycles talis et implications pour les analyses

Changement dans la définition de la population cible entre les cycles TALIS

Le troisième cycle de TALIS (TALIS 2018) permet d’analyser les changements sur une période de 10 ans. Néanmoins, une telle analyse pose des défis particuliers et requiert donc de la prudence. Les différents défis à relever sont les suivants : la couverture des pays et la population cible dans un pays donné peuvent différer d’un cycle à l’autre ; les variables d’intérêt peuvent changer, en outre, en raison de modifications des questionnaires ; de plus, le contexte de l’enseignement et de l’apprentissage peut également changer. Par conséquent, les comparaisons entre cycles doivent être interprétées avec prudence

Dans TALIS 2008, les enseignants dont l’enseignement s’adresse entièrement ou principalement aux élèves ayant des besoins spécifiques d’éducation ne faisaient pas partie de la population cible. Cependant, la situation a changé pour TALIS 2013 et 2018 avec l’inclusion des enseignants d’élèves ayant des besoins spécifiques d’éducation dans la population cible. Par conséquent, les estimations représentant le changement de 2008 à 2013 et de 2008 à 2018 doivent être interprétées avec prudence. Il est toutefois important de noter que les enseignants qui travaillent dans des établissements qui n’enseignent qu’aux élèves ayant des besoins spécifiques d’éducation ont été exclus de tous les cycles TALIS.

Dans le cas de la Nouvelle-Zélande, la définition de la population cible a changé entre TALIS 2013 et TALIS 2018. Alors qu’en 2013, les établissements comptant moins de quatre enseignants admissibles étaient exclus, ce n’est plus le cas en 2018. Par conséquent, une variable filtre (TALIS13POP), qui exclut les établissements comptant moins de quatre enseignants pour la Nouvelle-Zélande, a été utilisée pour estimer les statistiques de 2018 afin d’assurer la comparabilité des tableaux de données représentant les changements dans le temps. Par conséquent, ces résultats peuvent différer de ceux présentés pour l’ensemble de l’échantillon TALIS 2018 de la Nouvelle-Zélande, en particulier pour ceux fondés sur les déclarations des chefs d’établissement.

Modification des classifications CITE

La classification des niveaux d’enseignement repose sur la Classification internationale type de l’éducation (CITE). La CITE est un instrument qui permet de recueillir des statistiques sur l’éducation au niveau international. Dans TALIS 2008 et TALIS 2013, la CITE-97 a été utilisée pour rendre compte du niveau d’études des enseignants et des chefs d’établissement. La première classification, CITE-97, a été révisée et la nouvelle, CITE-2011, a été officiellement adoptée en novembre 2011. La CITE-2011 est la référence des niveaux d’études présentés dans les questionnaires TALIS 2018 destinés aux enseignants et aux chefs d’établissement. Les tableaux de données sur le niveau d’études des enseignants et des chefs d’établissement figurant dans le présent rapport sont fondés sur la CITE-2011. Un tableau de correspondance (tableau AII.B.1) a été utilisé pour traduire les catégories d’éducation de la CITE-97 utilisées dans TALIS 2008 et TALIS 2013 en catégories correspondant à la nouvelle CITE-2011, afin de produire des tableaux faisant état de l’évolution du niveau d’études des enseignants et des chefs d’établissement de 2008 à 2018. Ce tableau de correspondance a été utilisé pour compiler les tableaux I.4.11 et I.4.27 du chapitre 4 du volume I. Toutefois, l’évolution dans le temps du niveau d’études des enseignants et des chefs d’établissement devra être interprétée avec prudence en raison de la modification des classifications.

Tableau AII.B.2. Correspondance entre les niveaux CITE 2011 et CITE-97 utilisés dans les publications TALIS 2018

TALIS 2008	TALIS 2013	Catégories de la CITE-97	TALIS 2018	Catégories de la CITE 2011
CITE-97	CITE-97		CITE 2011
–	–	–	Niveau 0	Éducation préprimaire Fait référence aux programmes destinés aux jeunes enfants qui ont une composante d’éducation intentionnelle et visent à développer les compétences cognitives, physiques et socio-émotionnelles nécessaires à la participation à l’école et à la société. Les programmes à ce niveau sont souvent différenciés selon l’âge.
–	–	–	Niveau 01	Développement de l’éducation préprimaire
Niveau 0	Niveau 0	Enseignement préprimaire Première étape de l’instruction organisée, visant essentiellement à préparer les très jeunes enfants à un environnement de type scolaire.	Niveau 02	Enseignement préprimaire
Niveau 1	Niveau 1	Enseignement primaire ou premier cycle de l’éducation de base Normalement conçu pour donner aux élèves un solide enseignement de base en lecture, écriture et mathématiques.	Niveau 1	Enseignement primaire Conçu pour donner aux élèves un solide enseignement de base en lecture, écriture et mathématiques ainsi qu’une compréhension de base de certaines autres matières. Âge d’entrée : entre 5 et 7 ans. Durée type : 6 ans.
Niveau 2	Niveau 2	Premier cycle de l’enseignement secondaire ou deuxième cycle de l’éducation de base Le premier cycle de l’enseignement secondaire prolonge, en général, le programme de base du primaire, bien qu’il soit d’ordinaire plus axé sur les disciplines enseignées et suppose souvent l’intervention d’enseignants plus spécialisés qui donnent leurs cours dans leur domaine de spécialisation.	Niveau 2	Premier cycle de l’enseignement secondaire Il vient en complément du programme de base du primaire, généralement d’une manière plus axée sur les disciplines, avec des enseignants plus spécialisés. Les programmes peuvent varier selon l’orientation, générale ou professionnelle, bien que cela soit moins fréquent qu’au deuxième cycle du secondaire. L’entrée se fait à la fin de l’enseignement primaire et la durée type est de 3 ans. Dans certains pays, la fin de ce cycle marque la fin de l’enseignement obligatoire.
Niveau 3	Niveau 3	Enseignement secondaire de deuxième cycle Il s’agit de la phase finale de l’enseignement secondaire dans la plupart des pays de l’OCDE. L’enseignement est souvent plus organisé par discipline qu’au niveau 2 de la CITE et les enseignants doivent en général posséder un diplôme de niveau plus élevé, ou plus spécialisé, qu’au niveau 2 de la CITE1.	Niveau 3	Enseignement secondaire de deuxième cycle La spécialisation est plus forte qu’au niveau du premier cycle du secondaire. Les programmes proposés sont différenciés par orientation : générale ou professionnelle. La durée type est de 3 ans.
Niveau 4	Niveau 4	Enseignement post-secondaire non supérieur Ces programmes se trouvent, d’un point de vue international, à la limite entre le deuxième cycle du secondaire et le postsecondaire, même si, d’un point de vue national, ils peuvent clairement être rattachés soit à l’un, soit à l’autre de ces deux niveaux2.	Niveau 4	Enseignement post-secondaire non supérieur Il sert à élargir plutôt qu’à d’approfondir les connaissances, les aptitudes et les compétences acquises au deuxième cycle du secondaire. Les programmes peuvent être conçus pour accroître les possibilités offertes par le marché du travail aux participants, pour poursuivre des études supérieures, ou les deux. Habituellement, les programmes à ce niveau sont orientés vers la formation professionnelle.
Niveau 5	Niveau 5	Premier cycle de l’enseignement supérieur Les programmes de niveau 5 de la CITE ont des contenus d’enseignement plus approfondis que ceux proposés aux niveaux 3 et 4.	–	–
Niveau 5B	Niveau 5B	Les programmes de niveau 5B de la CITE qui sont en général plus pratiques/techniques/professionnels que les programmes de niveau 5A de la CITE.	Niveau 5	Cycle court de l’enseignement supérieur Il sert à approfondir les connaissances développées aux niveaux précédents par la transmission de techniques, concepts et idées nouveaux qui ne sont généralement pas couverts dans l’enseignement secondaire de deuxième cycle.
Niveau 5A licence	Niveau 5A	Les programmes du niveau 5A de la CITE qui sont largement fondés sur un enseignement largement théorique et axés sur l’acquisition de compétences suffisantes pour accéder à des programmes de recherche de haut niveau et à des professions exigeant de grandes qualifications.	Niveau 6	Niveau licence ou équivalent Conçu pour fournir aux participants des connaissances, des aptitudes et des compétences universitaires et/ou professionnelles intermédiaires menant à l’obtention d’un premier diplôme ou d’une qualification équivalente. Durée type : 3-4 ans d’études à temps plein.
Niveau 5A Master			Niveau 7	Niveau master ou équivalent Une spécialisation plus forte et des contenus plus complexe qu’au niveau licence. Conçu pour fournir aux participants des connaissances universitaires et/ou professionnelles avancées. Peut comporter un important volet de recherche.
Niveau 6	Niveau 6	Deuxième cycle de l’enseignement supérieur Ce niveau est réservé aux programmes du supérieur qui conduisent à l’obtention d’un diplôme de recherche de haut niveau. Les programmes sont consacrés à des études approfondies et à des travaux de recherche originaux.	Niveau 8	Niveau doctorat ou équivalent Conçu pour conduire à l’obtention d’un diplôme de recherche de haut niveau. Les programmes sont consacrés à des études approfondies et à des travaux de recherche originaux, et existent tant dans les domaines universitaires que professionnels.

1. Il existe des différences substantielles dans la durée type des programmes CITE 3, d’un pays à l’autre, allant généralement de deux à cinq années de scolarité.

2. Ils ne sont souvent pas beaucoup plus avancés que les programmes CITE 3, mais ils servent à approfondir les connaissances des participants qui ont déjà terminé un programme au niveau 3. Les élèves sont généralement plus âgés que ceux des programmes du niveau 3 de la CITE.

Source : UNESCO-UIS (2012_[1]), Classification internationale type de l’éducation : CITE 2011, Institut de statistique de l’UNESCO, Montréal, http://uis.unesco.org/sites/default/files/documents/international-standard-classification-of-education-isced-2011-fr.pdf.

Pour certains pays, la correspondance entre la CITE-97 et la CITE-2011 a été révisée pour tenir compte des spécificités nationales, par rapport à l’approche générale présentée dans le tableau AII.B.2.2. En conséquence, pour les tableaux I.4.11 et I.4.27, le niveau 5B de la CITE-97 a été reclassé au niveau 6 de la CITE-2011 pour l’Italie et la Communauté flamande de Belgique.

En Autriche, l’ancienne « Pädagogische Akademie » (académie pédagogique, niveau 5B de la CITE-97) a été transformée en « Pädagogische Hochschule » (collège universitaire de formation d’enseignants, niveau 6 de la CITE-2011) en 2007. Ainsi, dans le cas de l’Autriche, le changement important entre 2008 et 2018 des niveaux 5 et 6 de la CITE dans les tableaux I.4.11 et I.4.27 n’est pas seulement dû à la modification des classifications CITE, mais aussi au changement du système de formation des enseignants.

Au Portugal, les enseignants titulaires d’une « maîtrise pré-Bologne » sont classés au niveau 6 de la CITE. La question est présentée de manière à empêcher la désagrégation entre la « maîtrise pré-Bologne » et le « doctorat ».

En Slovénie, les enseignants titulaires d’une « licence pré-Bologne » sont classés au niveau 5 de la CITE (qui correspond habituellement à un enseignement supérieur de courte durée). La question est présentée de manière à empêcher la désagrégation entre la « licence pré-Bologne » et la « licence ».

Références

[2] OCDE (2019), TALIS 2018 Technical Report, Éditions OCDE, Paris, http://www.oecd.org/education/talis/TALIS_2018_Technical_Report.pdf.

[1] UNESCO-USI (2012), Classification internationale type de l’éducation : CITE 2011, Institut de statistique de l’UNESCO, Montréal, http://uis.unesco.org/sites/default/files/documents/international-standard-classification-of-education-isced-2011-fr.pdf.